这篇文章主要解决以下问题:
给出一组度数列,求解它们之间能否连成一个简单图,如何构成简单图?
前言
最近刚好在学SAS,尝试性地写了一个程序去解这个问题:给一组点的度数列,求解它们之间能否连成一个简单图。
虽然本意是写一个判断一组度数列能否简单图化的程序,完成之后发现这个程序比起判断可行性,还是在有可行解的情况下给出可行解比较快——只要你输入的度数列是能简单图化的,它给出答案的速度非常快;但如果给它一组不能简单图化的度数列(最经典的方法就是违反握手定理),它计算出结果的速度会很慢。
实现
- 这是求解程序 (简单图分析.sas)
data degree;
input degree @@;
datalines;
3 3 2 2 2
run;
proc optmodel;
set<num> POINT;
num Degree{POINT};
var Link{POINT,POINT} BINARY;
con Full_Link{p in POINT}:sum{q inPOINT}Link[p,q]=Degree[p];
con No_Link{p in POINT}:Link[p,p]=0;
con Symmetry{p in POINT,q inPOINT}: Link[p,q]=Link[q,p];
max Best=sum{p in POINT,q inPOINT}link[q,p];
Read data degree into POINT=[_N_] Degree;
solve;
Print Link;
quit;
- 这是 matlab 上的问题生成程序:生成一个随机简单图 (make_simple.m)
%% 随机生成一个简单图的邻接矩阵
function a=make_simple(n)
a=floor(rand(n,n)*2);
[m n]=size(a);
for i=1:m
for j=1:n
if i>j
a(j,i)=a(i,j);
end
if i==j
a(i,j)=0;
end
end
end
end
- 这是 matlab 上的解答验证程序:判断一个邻接矩阵是否是简单图 (is_simple.m)
%% 检验一个邻接矩阵是否为简单图
%% 如果有两个参数,自动修剪掉矩阵的第一行和第一列
function bool=is_simple(a,b)
if nargin==2
a=a(2:end,2:end);
end
ok1=0;ok2=0;ok3=0;
if sum(sum(a<0))==0
ok1=1;
end
if sum(diag(a))==0
ok2=1;
end
if a==a'
ok3=1;
end
if ok1*ok2*ok3==1
bool=1;
else
bool=0;
end
end
求解
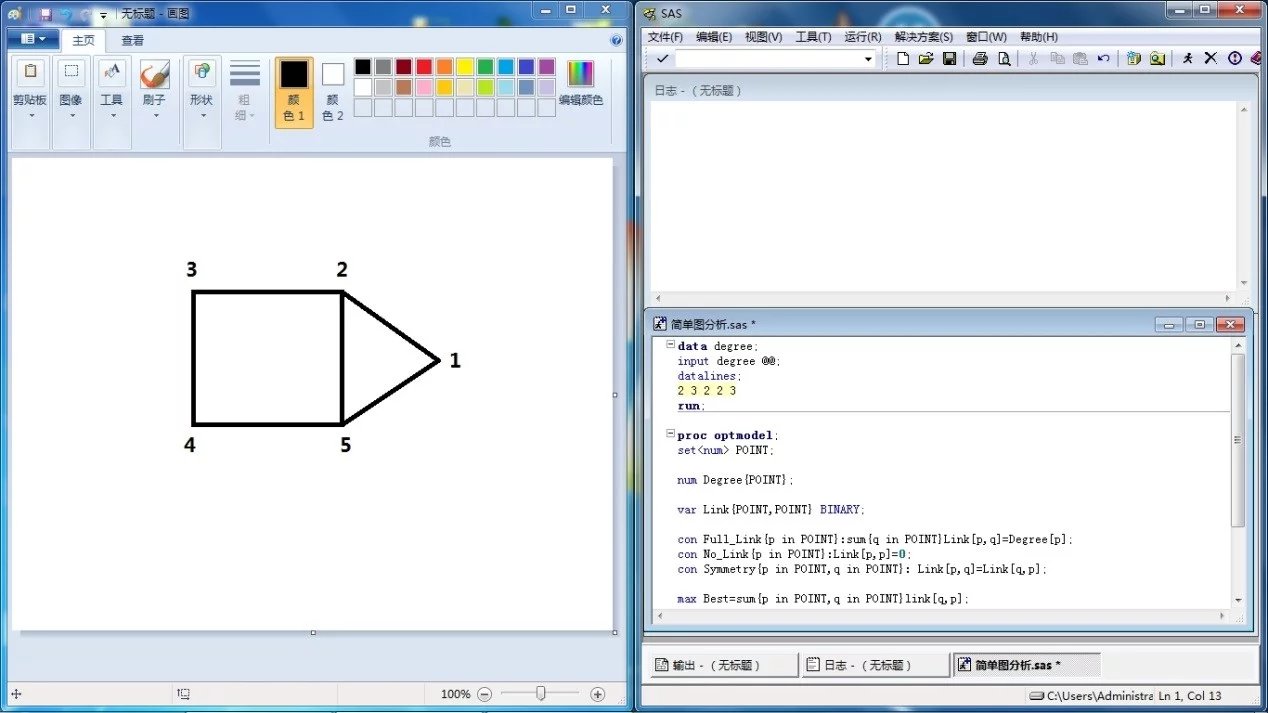
假设简单图模型如下
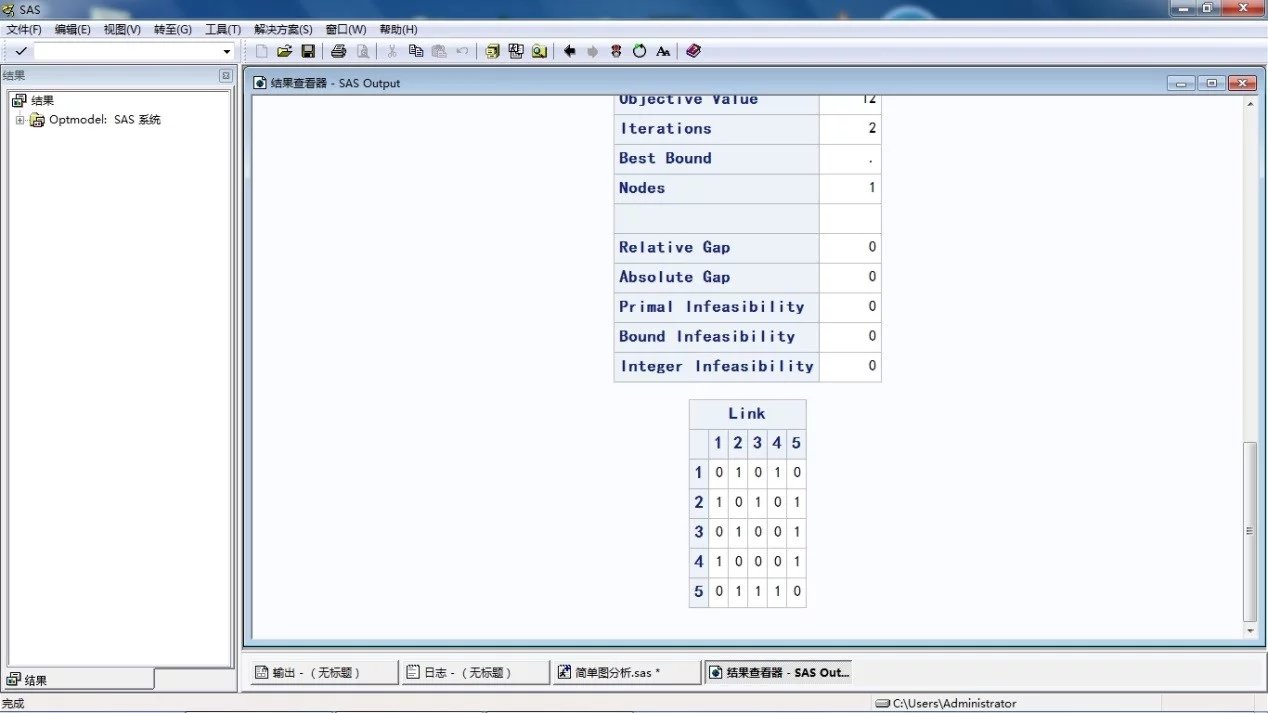
运行求解
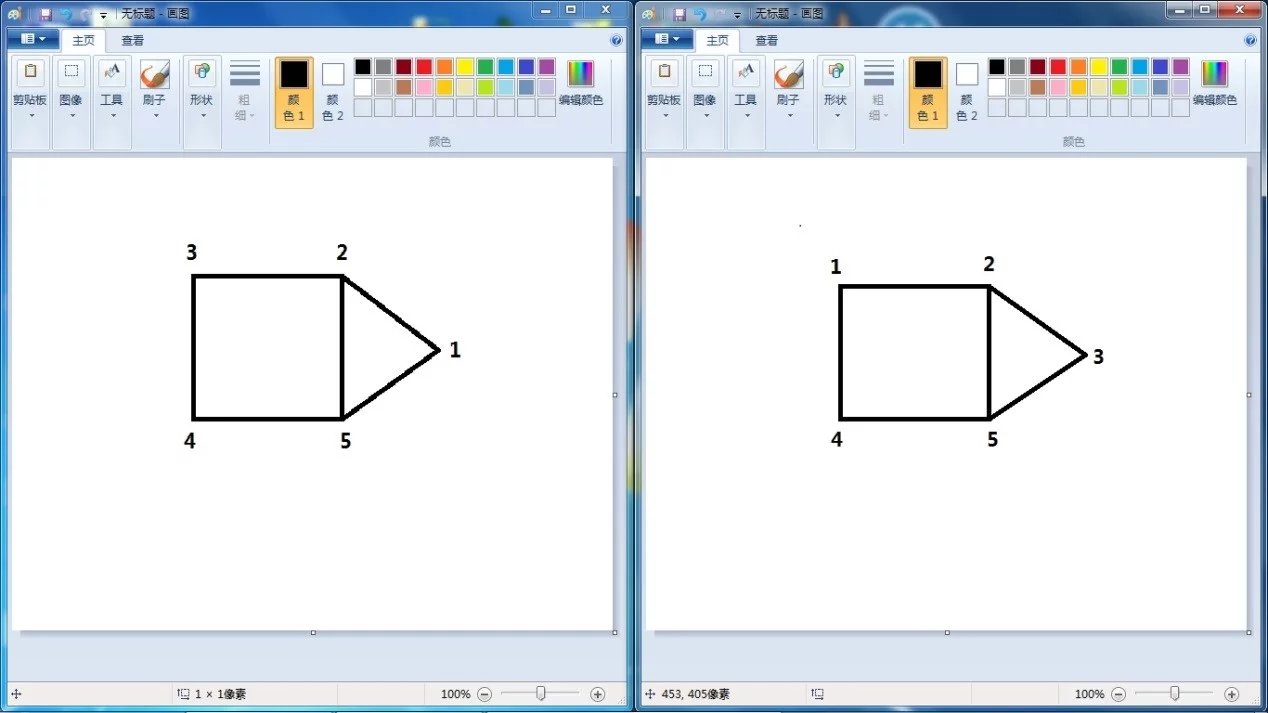
将实际情形与 SAS 给出的答案画出来对比,能看出两者其实是等价的。
算法测试
鉴于更高维度的简单图手工构造实在有难度,这里采用邻接矩阵的模型,用 matlab 模拟一个大规模的简单图(生成程序见上)
生成简单图的思路是:先随机生成一个 0-1矩阵,然后把它修正成一个简单图
先随机构造一个 50 个顶点的简单图
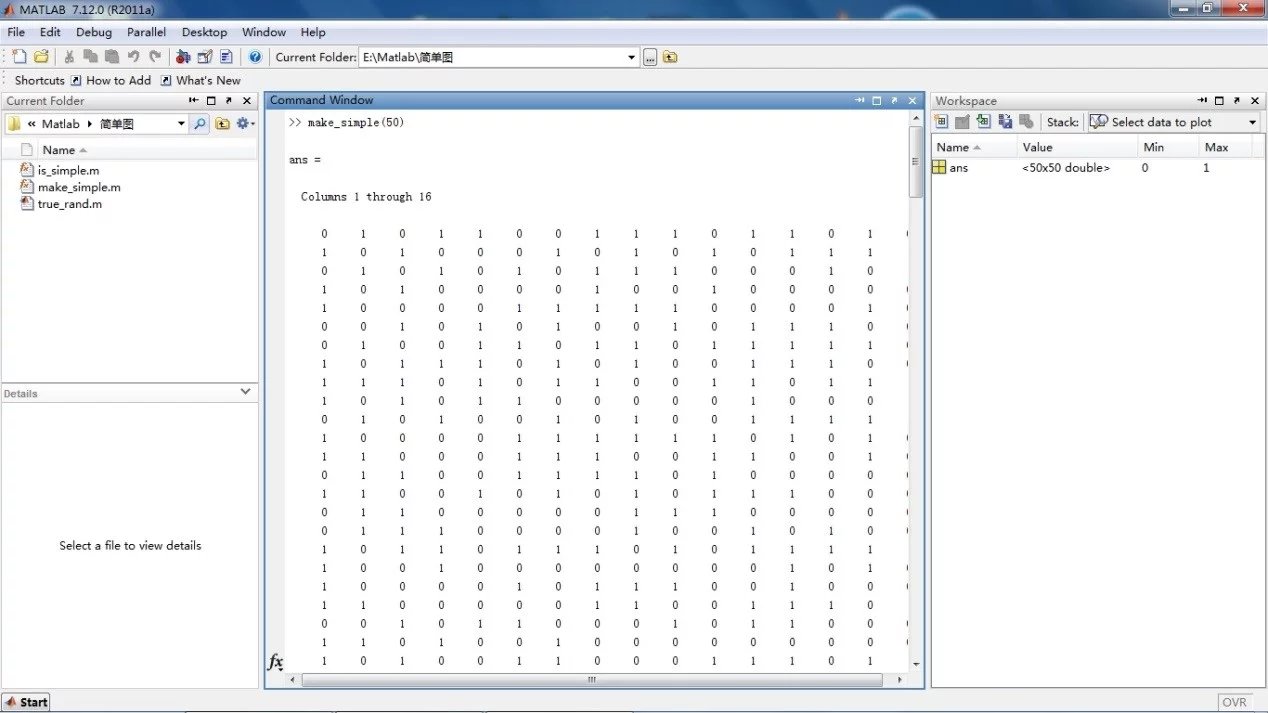
获取度数列
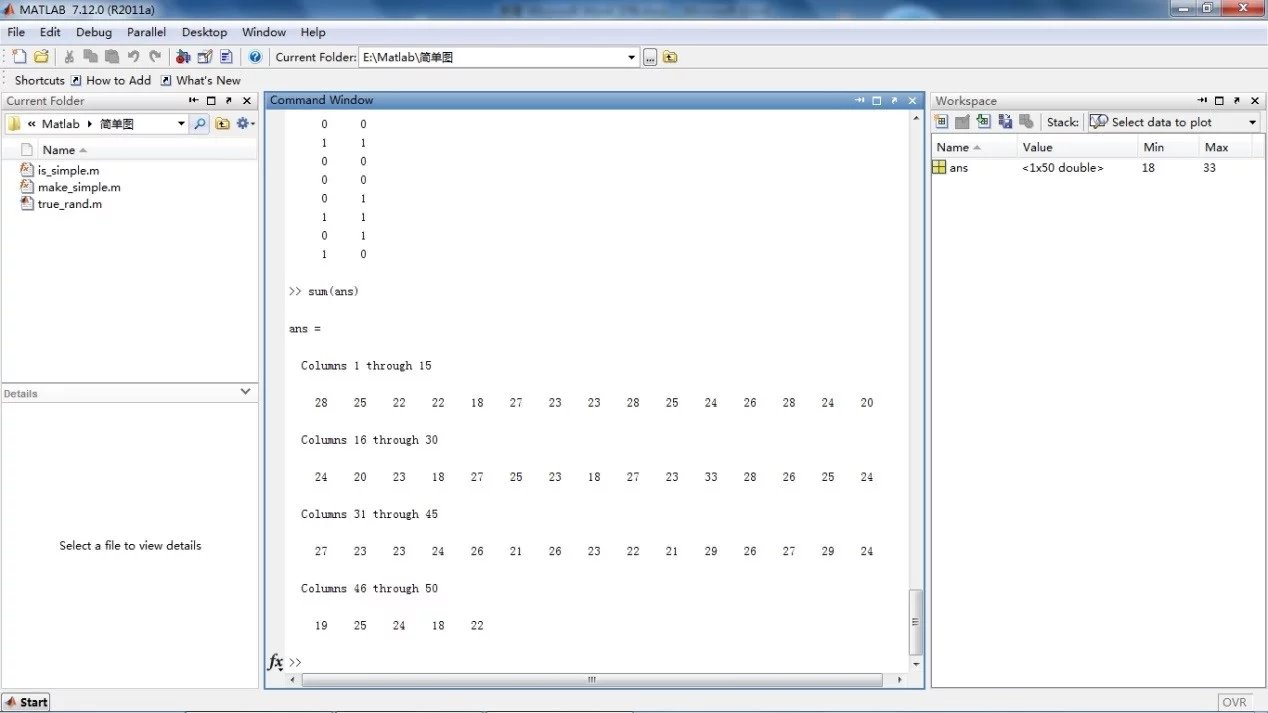
输入 SAS
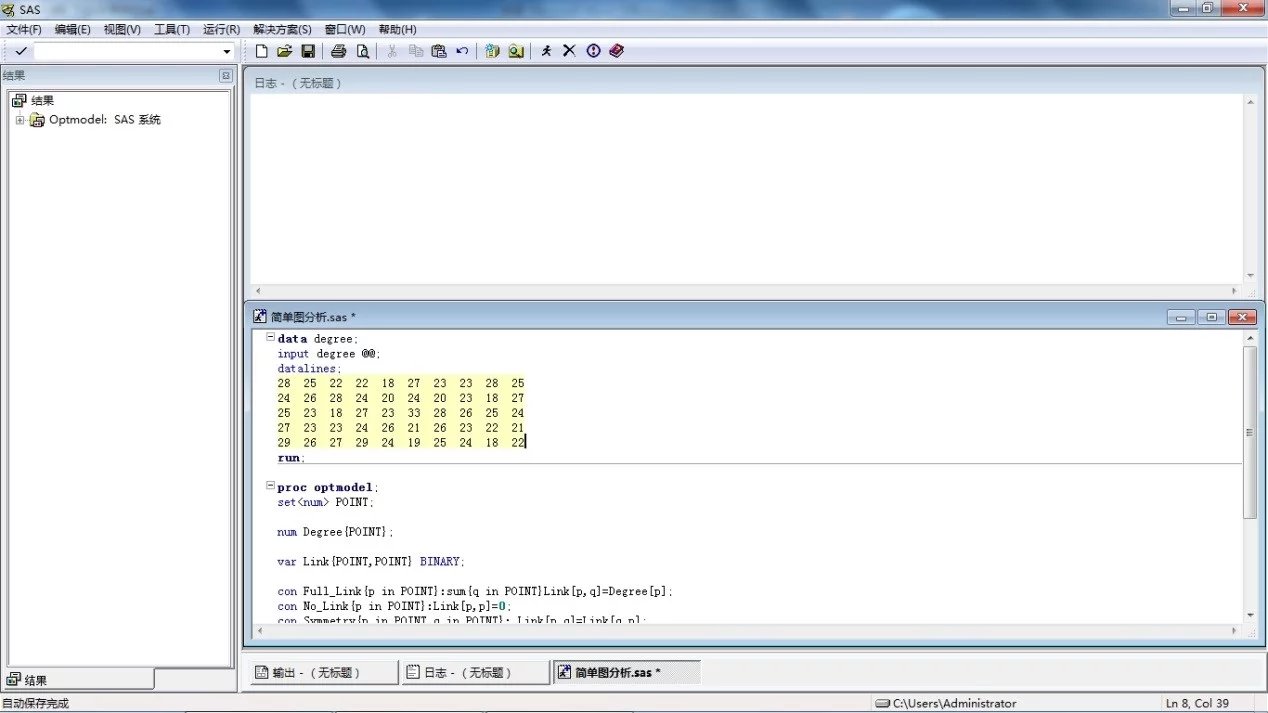
求解结果,不到 1 秒就算出答案了
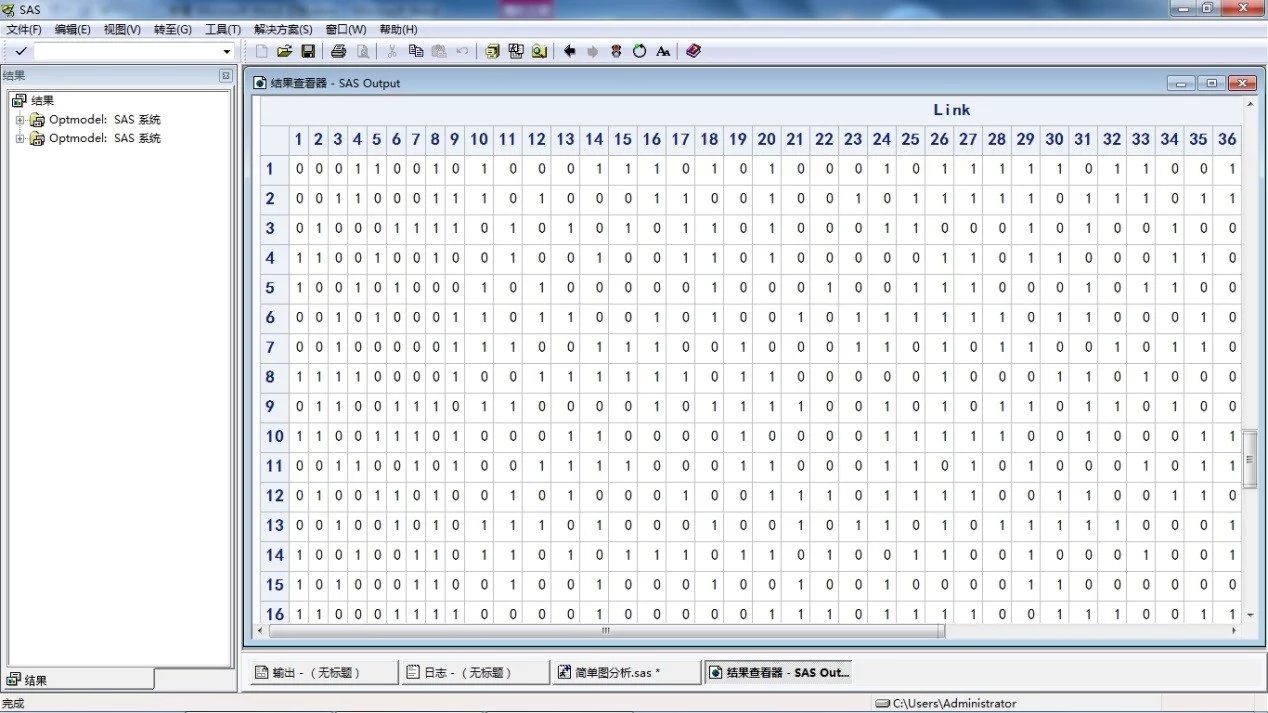
答案是不是简单图,还需要检验。还是用 matlab 测试(检验程序见上)
检验方式是:看它给出的矩阵对角线是否全 0,是否对称,是否只有 0-1两种元素。
结果证实了 SAS 所给的简单图,确实是简单图
暂无评论