本文主要解决这个问题
假设一个密文是用未知长度的异或密钥加密,如何求异或密钥长度?
卡西斯基检验法
寻找密文中重复出现的子串,计算它们之间距离的最大公约数
因为同一明文片段若经过相同相位的密文片段加密,会产生相同密文。此时密文里对应的重复片段间隔,刚好是密钥长度的整数倍。所以反其道而行之,统计密文里所有重复出现的子串与重复距离可作为突破口
一般来讲,选择 3-gram 或 4-gram 的子串作为特征搜索
IC 检验法
1、双射变换不改变频率分布
单字节异或加密作为可逆的单表替换,是一种双射变换,即:
- 假设明文里所有 A 都加密成 X,那么密文里所有 X 也只能来源于 A
- 假设明文里所有 B 都加密成 Y,密文里所有 Y 也只来源于 B
因此,明文中 A 的出现次数和密文中 X 的出现次数是相同的,明文所有 B 的出现次数跟密文所有 Y 的出现次数也相同
将每个字节的频率排成向量,就会发现,明文各个字节的频率向量,和密文各个字节的频率向量,是重排序的关系。即各字节按频率大小排序后,画出的频率分布图形状是一样的
向量之间的比较和描述不太方便,因此基于频率分布图算一个统计量,把它压缩成数值。其中一种方式是算 IC,定义
$$ IC = P(00)^2 + P(01)^2 + ... + P(FF)^2 $$
那么,异或加密前后,明文和密文的 IC 值不变
2、多表替换可拆为多个独立的单表替换
多字节异或加密是一种多表替换,异或密钥的每个字节各对应一个单表替换
假设既有明文又有密文,只要明文和密文分别按照异或密钥的长度分组,那么每一组内的明文和密文,刚好落在同一个单表替换里,这时每组明文和每组密文的 IC 值相等
3、IC 统计量的特点
IC 的现实意义,相当于从一个二进制文件里随机抽 2 个字节,这两个字节相同的概率。
无论是从英文上 IC = Index of Coincidence,Coincidence = 巧合,还是从中文上 IC = 重合指数。这里“巧合”跟“重合”都跟上面的现实意义很好地对应
研究一下 IC 的最大和最小值。根据定义,相当于:
已知
$$ \sum_{i=0}^{255}x_i = 1 $$
求
$$ ic = \sum_{i=0}^{255}x_i^2 $$
的最值
显然
- 当任意一个 x_i 为 1 时,其余 x_i 必为 0,此时 IC 最大,取值为 1
- 当所有 x_i 相等,都等于 1/256 时,此时 IC 最小,取值为 1/256 ≈ 0.004
可见,分布越极端,IC 越大,分布越均匀,IC 越小。这在现实意义上也很好对应,当球堆里只有一种颜色的小球时,任意摸 2 个,得到同色球的概率是 1。而当均匀分布的时候,模同色球概率最低。
4、自然语言/DSL 的 IC 值偏大
- 像自然语言,DSL 等有明确意义的明文,字节的分布往往是有偏好的,所以 IC 值偏大
- 一段没有意义的随机字节,字节分布认为是均匀的,如上所述,IC 值最小
比如,这是一篇英语文章的频率分布。可以看到 0x20(空格)字节最多,然后是 0x65(字母 e),IC 值是 0.07
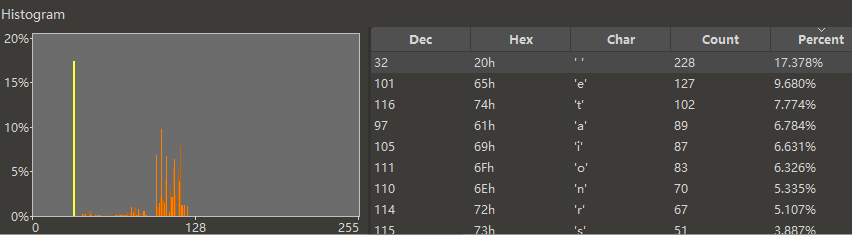
这是一段日语文本的频率分布。可以看到 0x82(所有平假名公有的首字节)断档地最多,IC 值是 0.054
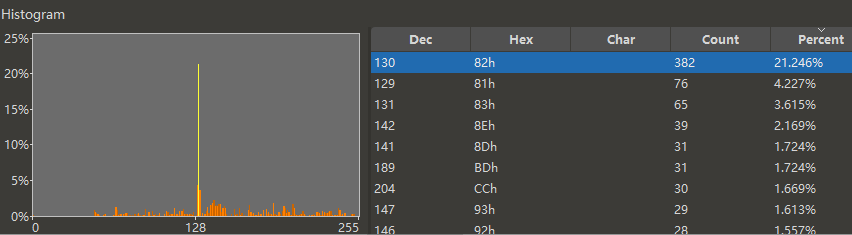
因为游戏的脚本文件本质是一种 DSL,所以 IC 值也很大
这是 Yuris 引擎的一个解密后的游戏文件。可以看到 0x00 断档地最多,然后是 0x01,0x82,IC 值是 0.203
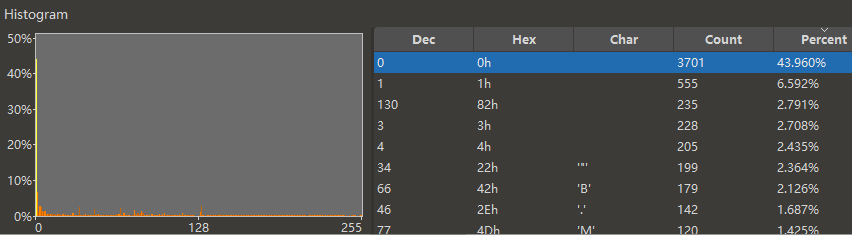
5、IC 检验法
综合上述四点,我们可以在未知明文的情况下,只靠密文推算异或密钥周期
- 分别按照 T = 1,2,3,4… 的间隔给密文分组
- 对每个分组里的密文算 IC 值取平均,平均 IC 值越大,说明它不是随机分布的概率越大。
- 遍历每个分组间隔对应的平均 IC 值,只要分组间隔跟密钥的周期一致(或等于周期的整数倍),就会观察到 IC 极大值。
- 每个显著的 IC 极大值点,对应的间隔 T 都可猜为候选密钥
之前 Yuris 引擎密钥新解 里,同样的加密文件,假设我们不知道 Yuris 引擎是四字节异或加密,可用这个方法猜密钥周期:

结果完全正确!这样一来,Yuris 引擎密钥新解 最后的结论可以再更进一步:
一路下来我们一不开游戏,二不起 OD,
只知道文件是 4 字节密钥异或加密结果,只知道文件是某个未知长度的密钥异或的结果,用统计分析加一些计算,就能把密钥破了
6、推广
除了异或加密,从原理看,任何多表替换加密,只要每个表都是双射变换,都可以用 IC 检验法分析出周期
之前 用 GF(2) 仿射模型破解一类文件加密算法 有一个遗留问题,假设加密黑箱可以复合为 y = Ax + b,偏置项对应的密钥长度未知的时候,怎么求密钥长度?
现在来看,因为仿射变换要可逆的话,x 和 y 必须是双射,所以这个方法完全适用。只要 x 是自然语言或脚本 DSL,我们一样可以用 IC 法计算周期
卡方检验法
IC 检验法,从我们得到频率分布图之后,将频率向量压缩成一个数值之前,这里实际上存在另一种做法
我们不算每个频率的平方和,改算卡方
卡方的定义
自然语言有自己每个字节的频率分布。随机取样另一个文件,样本同样有自己每个字节的频率分布
卡方检验就是计算两个频率分布图像不像,越像越小,越不像越大。卡方就是偏差度
$$ \chi^2= \sum_{i=1}^{n}\frac{(O_i - E_i)^2}{E_i} $$
举上面的例子,这是一篇英语文章每个字节的频率分布

以它为标准,我们给三个样本
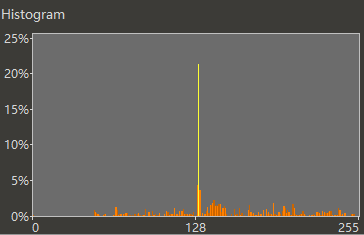
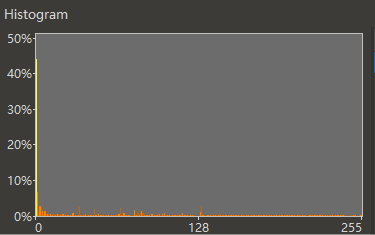
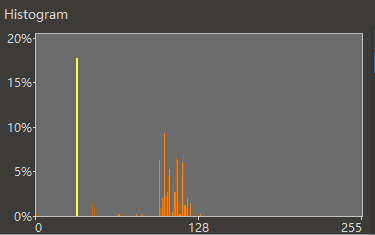
样本一和样本二跟标准频率分布不像,卡方很大。事实上它们分别是日语文本和游戏脚本。样本三跟标准频率分布高度相似,卡方就很小。它是我随机另生成的一段英语文本
假设我们已知明文那类文件的标准卡方分布是什么。也可以用类似 IC 检验的那套流程对密文不断分组,猜卡方突减点为周期。但实际上卡方检验法往往不用来猜周期,它的强项是已知周期的时候求单表替换加密的密钥。
单表替换密码,解空间每个候选密钥对应一个卡方,可将卡方作为目标函数,用爬山或模拟退火,求一个最优解作为密钥
自相关分析
这里的相关并非数值计算上的相关,是相等意义上的相关。比如,固定一个间隔 k,如果第 i 字节跟第 i + k 个字节一样,就说这两个字节相关
假如一份数据完全随机,那么第 i 个字节和第 i + k 个字节两者相等的概率是 1/256 ≈ 0.4%。反过来,如果数据是自然语言或 DSL,第 i 个字节和第 i + k 个字节两者相等的概率不会这么均匀,哪怕大一点点(比如 0.6%)就足以说明问题
定义
$$ R(k) = \sum_{i=0}^{N-1-k} \frac{1}{N-k}( x_i == x_{i+k} ) $$
多字节异或生成的密文,分别代入 k = 1, 2, 3, … 算自相关值,当 k 不等于密钥周期时,结果跟随机取字节没什么差别。当 k 恰好等于周期(或其整数倍)时,每个 x_i 和 x_{i+k} 总处在相同的双射表,自然等于明文的 R(k) 自相关值,这时会观察到 R(k) 突增。据此求出密钥周期
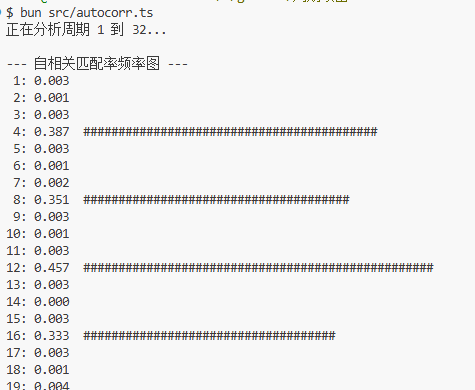
汉明距离法
汉明距离,指的是两个等长比特串中,不同比特的个数
$$ d_H(x, y) = \sum_{i=0}^{N-1} (x_i \oplus y_i) $$
汉明分数,指的是归一化的汉明距离。因为汉明距离会随着比特串长度增加而增加,所以我们要除以比特串长度
$$ d_H(x, y) = \frac{1}{N}\sum_{i=0}^{N-1} (x_i \oplus y_i) $$
两个随机字节之间,汉明距离平均为 4
因为八个比特位是否相同是独立的,相同的概率是 1/2,所以平均汉明距离:1/2 * 8 = 4
自然语言两个随机字节之间,汉明距离一般小于 4
比如 [a, z] 里,随机两个英文字符的 ascii 编码 [61, 7A],平均汉明距离仅为 2.57
假设周期为 T,将密文分别错位 1, 2, 3, … 个字节跟自身算汉明分数,如果错位字节数刚好等于周期(或整数倍),可观察到汉明距离突减

代码
把整篇博客输入 AI,很快就帮我生成了整个项目。输入一个密文,它可以用上面 4 种方法算出周期
https://github.com/dantecsm/periodic-attack
IC,自相关和汉明距离法的底层原理
无外乎三点:
- 随机字节与自然语言/DSL 在某个统计量上显著不同
- 双射的单表替换不改变该统计量
- 多表替换若以周期为间隔分组可拆成多个独立的单表替换
展开来讲,假设 A 加密为 X,B 加密为 Y,即
A ↔ X
B ↔ Y
那么,加密前后:
- IC 统计量相等:因为频率分布图没变,只是打乱标签而已,P(A)² + P(B)² = P(X)² + P(Y)²
- corr 统计量相等:因为 A == B 时,必有 X == Y,反之亦然,所以 A == B 的个数和 X == Y 的个数相等,所以自相关值相等
- 汉明距离相等:H(X, Y) = bitSum(X ^ Y) = bitSum(A ^ B) = H(A, B)
从以上可以看出:IC 法和自相关法只要是双射的单表替换加密都可以,而汉明距离法只适用于异或加密,因为它基于 X ^ Y == A ^ B
下面介绍一些我在研究时一些本不是为了解决这个问题,但额外发现的实用技巧
额外1、SJIS 编码特性
随便下载一个 SJIS 文本,发现 0x82 的占比很高,在 256 字节统计中占 21.246%
因为 0x82 是所有平假名的第一字节,每个平假名都贡献了一个 0x82 字节,导致刷票,如图
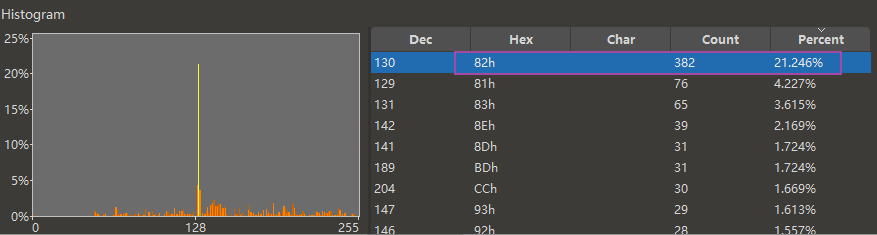
某种程度上讲,可以搜索 /(\\x82[\\s\\S]){2,}/g 在文件中的匹配次数/长度作为一个文本是否已解密为 sjis 明文/是否为 sjis 编码的一个判断依据
额外2、频率统计法速通异或密码
利用 0x82 高频出现的特点,可以快速破解单字节异或加密的 sjis 游戏脚本
实战1:Nangoku Domination
010 Editor 打开一个子文件 pro.box,点击 Tools → Histogram → OK,看到
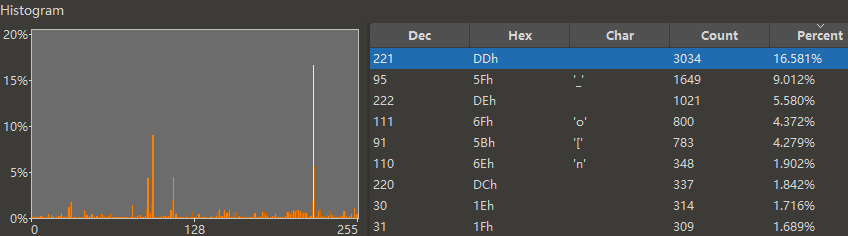
最高频字节是 DD,猜它是 0x82 的异或结果,于是密钥 = DD ^ 82 = 5F
用 5F 对原文件异或,果然看到大量合理的 sjis 明文
实战2:EVE Burst Error Win 版
这个游戏之前我逆向过,具体细节在EVE Busrt Error Win 逆向心得
- 第一次:我是用 Api Monitor 监控文件读取记录,在 ReadFile 处找到待解密的密文内容,下硬件断点,跟跑汇编,知道它是取反,即异或 FF 加密
- 第二次:我是读取一节明文,用 01-FF 分别异或这节明文,到密文里搜索,只有 FF 加密过的明文才能搜到结果,所以知道它是异或 FF
现在有了又快又省力的第三种方法
英化脚本 a001.sco,010 Editor 查最高频字节是 DF。因为英语理论最高频字节是 20,所以 DF ^ 20 = FF → 正确
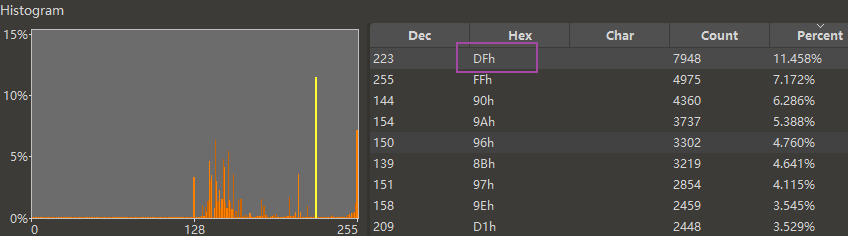
日语脚本 a001.sco,010 Editor 查最高频字节是 7D。因为日语理论最高频字节是 82,所以 7D ^ 82 = FF → 正确
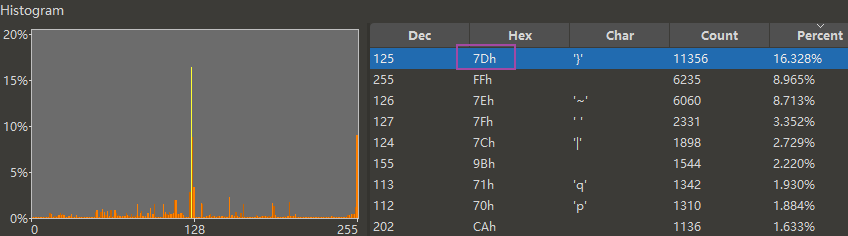
实战3:Yuris 引擎密钥破解
多字节异或的情况,可以先用 IC/自相关/汉明距离算密钥长度,然后把密文按密钥长度分组,每组内分别转成单字节异或的情况去解
上文中,在 IC 检验法里刚好测过 Yuris 引擎脚本的明文分布,知道 0x00 是理论最高频字节
Yuris 引擎的一个解密后的游戏文件。可以看到 0x00 断档地最多,然后是 0x01,0x82,IC 值是 0.203
在 Yuris 引擎密钥新解 中,我曾算出一个游戏文件的密钥是 D36FAC96
同样的游戏文件,现在把它按 4 字节间隔拆成 4 个子文件,然后分别对每个子文件统计最高频前 5 字节,与理论最高频字节 00 异或。结果出乎意料地好,每个子文件最高频字节异或 00,刚好完整组成正确密钥——
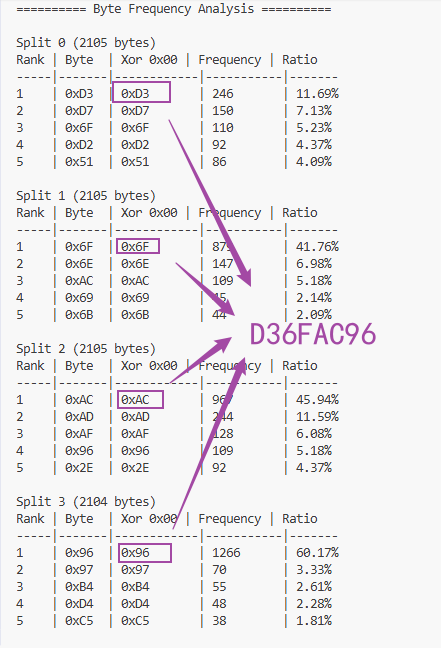
现在破解 Yuris 密钥,又有了一种方法
暂无评论