汇编就是有向图
软件破解中，VM 始终是汇编分析的一个难点
某天晚上，在破解了一个软件的验证机制后，我突然意识到：汇编的结构本质就是一个有向图——顺序指令是单箭头，分支指令是双箭头。假设要破解的目标位置为终点；当前位置为起点，本质上就是找一条路，把沿途所有错误的分支砍了，让它一路走到我们想要的位置
“关键跳”为什么有用
举个例子，一个游戏必须在输入框输入正确的认证码后打开，那么一般 CreateWindow 就是终点，认证码输入处下断点，断点处的汇编就是起点
破解这个认证流程，一般是找到汇编里的几处指令把它 NOP 掉。从而实现无论输入的认证码正确与否，它都会跳到只有认证成功才会进入的汇编继续执行。这样的指令被称为关键跳
可以发现，NOP 掉关键跳的做法，本质上就是在砍有向图中的错误分支。就像走一个山洞迷宫一样，穿过一个洞口可能会遇到两个洞口，也可能遇到一个，我们知道总有一条路会通往终点
修改关键跳，就是把关键双洞口处会诱导我们走错的那个给封住
问题的提出
给定一个有向图，该图所有节点出度≤2，指定一个起点和一个终点（假定起点可达终点），求：
至少从有向图上删除哪几条边，可保证从起点出发必达终点
问题的解决
问题的简化
从一个起点出发，有向图中所有点分为起点可访问的点和不可访问的点。显然，起点不可访问到的部分对这个问题没有影响
我们可以从起点出发，做一次 BFS/DFS，根据可访问到的点集，做原图的子图。以这个有向图替换原问题的有向图，继续提相同的问题
在一个有向图中，指定终点，那么图上所有点可分为两类
- 一类是可以到达终点的点，下称
可达点（注意：可达是指可能到达，有路但不是必达） - 一类是不可能达到终点的点，下称
不可达点
显然，有向图中每条应该删除的边，它们的每个起点都是符合上文定义的关键跳
下面不加证明地给出一个结论：
一个节点是关键跳，当且仅当符合以下条件：
1. 该节点是可达点
2. 该节点的出度为 2
3. 该节点的 2 个后继节点中，其中一个是可达点，另一个是不可达点（此结论可通过反证法证明，这里不展开）
可见，只要能分辨图上每个点是可达点，还是不可达点，就能找到所有应删除边的起点
因此，问题转化为：
给定一个终点，如何确定有向图上哪些点是可达点，哪些点是不可达点？
很容易想到的一个方法是 BFS/DFS，即对图上每个点做遍历，看每个点能访问的集合中是否包含终点
但这样的效率太低了，复杂度大约是 O(n(n+m))，在大图上难以接受。
下面引用一个概念：逆图
一个有向图的逆图，指的是：原图中所有节点不变，但所有边的方向取反，得到的新图具体做法如下：
- 先做原图的逆图
- 逆图上，从终点出发做一次 BFS/DFS。该点出发所有可遍历到的点记为 1，其余点记为 0
- 逆图上所有记为 1 的点，对应到原图上，就是对终点的
可达点；所有记为 0 的点，就是原图上对终点的不可达点
这样一来，只需一次遍历，复杂度就降低到 O(n+m)，比逐点做搜索高效得多。
至此，子问题解决完毕
知道了怎么划分有向图上的可达点和不可达点，我们就可以借助上节的结论找到所有关键跳节点
已知关键跳的 2 个后继节点，一个是可达点，一个是不可达点。显然，有向图上所有应该删除的边，就是所有关键跳节点的通往不可达点的边
至此，原问题解决完毕
下面总结完整的方案：
设有向图为 F，起点为 s，终点为 t
1. F 上从 s 出发 BFS，以 BFS 结果点集作出 F 的子图 G
2. 作 G 的逆图 G'
3. G' 上，从 t 出发 BFS，找到 G' 中所有 t 可访问的点。把可访问的记为 1，不可访问的记为 0，同步给 G
4. 定位 G 中所有以下特征的点：有 2 个后继节点，其中一个后继节点是 0，另一个后继节点是 1。记为点集 K（关键跳）
5. 点集 K 中，所有连接后继节点为 0 的边的集合，即为所求图的 BFS 算法复杂度一般是 O(n+m)，考虑到这里每个点出度≤2，可以简化为 O(n)。上面的算法，分别从起点和终点各做了 1 次 BFS 和 1 次全点遍历，因此复杂度是 O(n)
举例
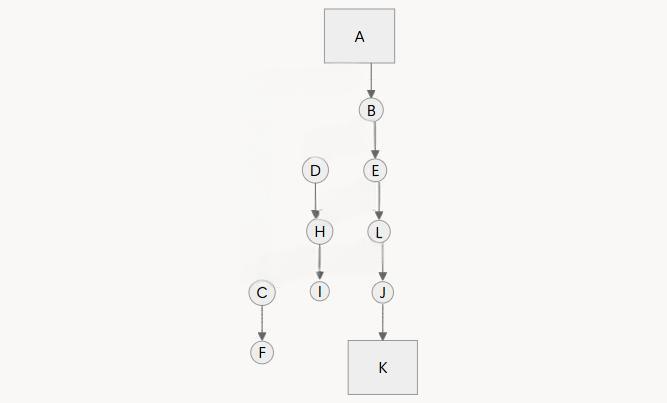
如图，假设 A 为起点，K 为终点
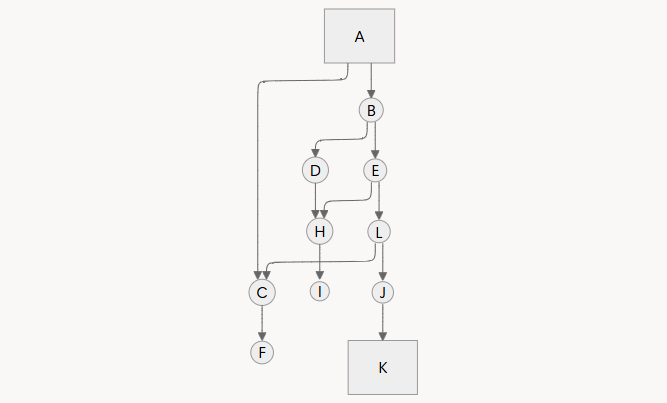
起点 A 可达图中所有点，因此子图不变
假定原图所有箭头方向取反，终点 K 可达 J、L、E、B、A，这几个点记为 1，其余为 0
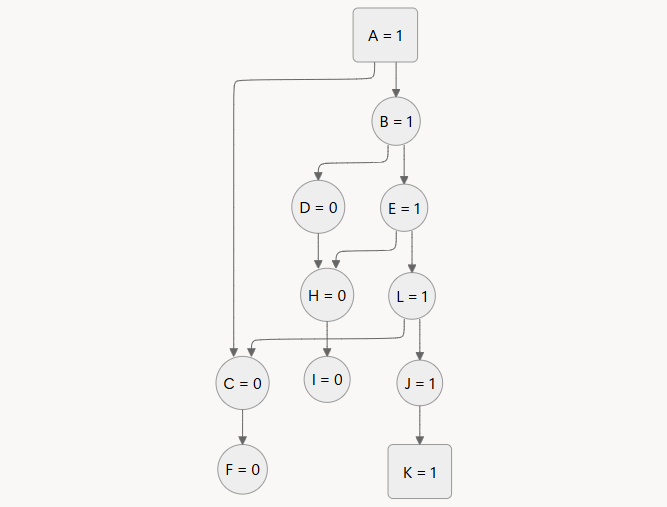
扫描所有出度为 2 且值为 1 的点，得到 A、B、E、L，再筛选其 2 个后继节点值互异的，得到 A、B、E、L，这就是关键跳
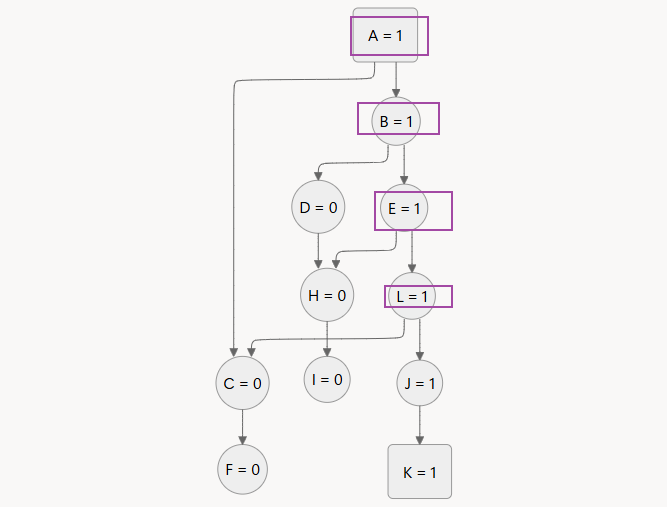
关键跳里面，删除所有通往 0 的边 A→C、B→D、E→H、L→C
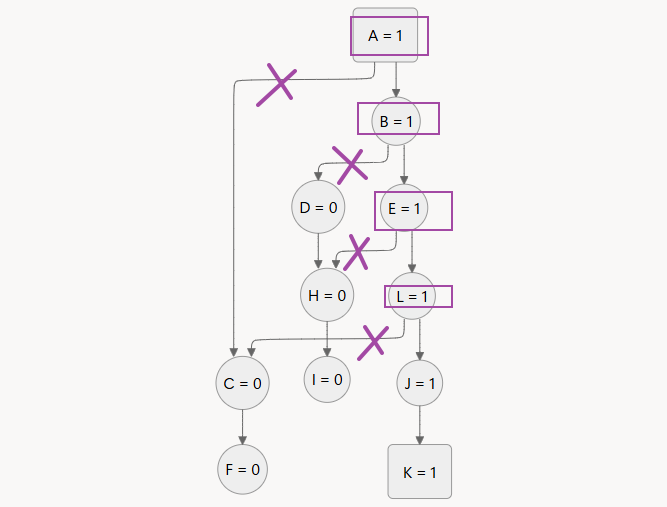
那么，起点 A 和终点 K 之间，就从可达关系变成必达关系
这也是软件破解时，干掉关键跳为什么有用的直观图示
从数据结构到汇编语言
上面讲的比较抽象，回到实际汇编讲讲对应关系
一、关键跳对应汇编的什么？
以 x86 为例，我们可以把所有指令分成三类：
- 第一类是顺序指令，比如 MOV、ADD、PUSH、CMP，出度为 1
- 第二类是跳转指令，就 JMP、CALL、RET 三种，它们的特点是单向跳转，出度为 1
- 第三类是条件跳转指令，比如 JZ、JL、JNE、JGE，它们的特点是双向跳转，出度为 2
按照出度分类，其实就条件跳转指令和其它指令两类，前者是双洞，后者是单洞
关键跳的总是出现在出度为 2 的地方，因此总对应条件跳转指令
二、删除有向边对应汇编的什么操作？
条件跳转指令的两条边，满足条件时触发跳转；不满足条件时顺序执行
因此，当我们删除条件指令一条边的时候，分为两种情况：
- 如果删的是触发跳转的边，就是把指令改成
NOP - 如果删的是顺序执行的边，就是把指令改成
JMP
NOP 的机器码是 90，JMP 的机器码是 EB 或 E9。同等条件下，无论改成哪个，它们的字节数总是少于或等于条件跳转指令
逆向软件时，由于低级语言的可读性很差，逐条追踪汇编是相当费劲的，特别是一些 VM，还让汇编变成几乎不可理解的状态
而把汇编转成有向图，从图的结构定位必经之路和关键节点，某种程度上可以自动化分析。比如上面的有向图，想象它的每个节点是一条汇编。哪怕它的规模成千上万，逻辑关系茫茫复杂。我们都不用理解它里面哪怕一行代码，直接从拓扑结构上完成破解
显然，一个软件如果可以通过修改关键跳破解（或已处理成能修改关键跳破解的情况），那么它修改的地方，必是上面方案中点集 K 的子集。我们可以在所有分析出来的所有关键跳处下日志，或者直接生成整个 PC 日志，定位第一处进入不可达点的关键跳。修改测试。成功的话，这就是最小可行补丁，否则继续相同的流程，直到成功为止。
汇编有向图的简化
一个软件里的汇编指令成千上万，转成有向图去分析的话就有同等数量的节点，规模显然很大
有没有办法简化呢？答案是 CFG（控制流程图）
比如，IDA 的流程图就是。如图所示，每个基本块，都是把汇编中那些单向通路的指令都压缩成一个“点”。而且每个基本块的出度，要么是单箭头要么是双箭头。整体刚好也是一个出度不超过 2 的有向图，分析方法跟前文是一样的。
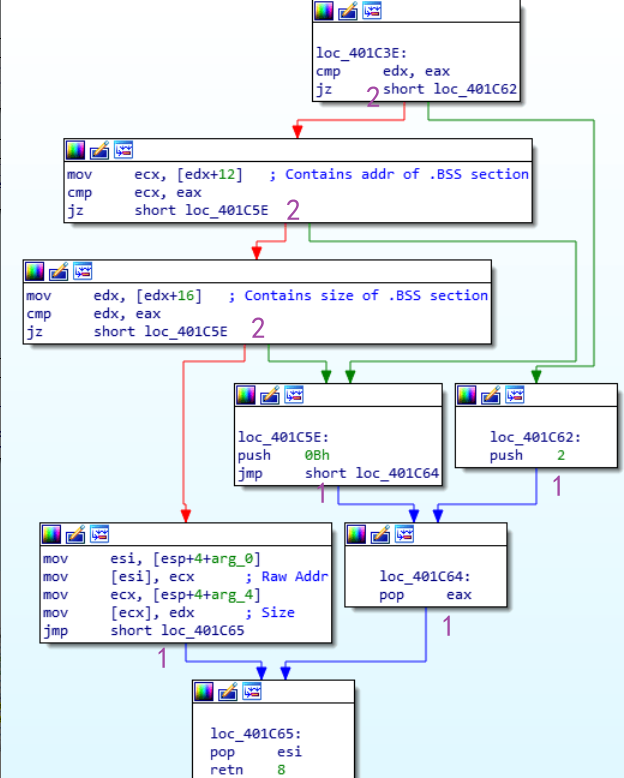
这种流程图其实是通过
CFA(控制流分析) 技术生成的，感兴趣可搜索《编译原理》相关章节，不再赘述
暂无评论