起因

崩铁仙舟地图上有一类出勤率很高的小游戏《罗盘引航》，玩法是拧三个操作杆转动三个圆环里的指针，让它们最后同时指向给定方向。

像初版《生化危机4》，《第七位访客》还有 3DS 的《善人死亡》都有类似的谜题，因为数量很少，每次我都是靠猜的。但这次不一样，仙舟地图里这种谜题实在太多了，有的还相当有难度。因此我决定静下心来，专门研究一下此类游戏对策。

游戏规则

罗盘有三个圆环，从内到外分别是内环、中环和外环。每个环上都有一个指针，游戏目标是让三个指针全部指向同一个方向。

虽然不同游戏的细节可能不同，但基本规则是：

• 游戏提供三种操作按钮，每个按钮会同时转动一个或两个环
• 每个环的指针都有固定的转动周期，转动一定次数后会回到起点

以其中一个游戏为例，具体规则可以是：

• 操作一：内环和中环同时逆时针转一步
• 操作二：中环逆时针转一步，外环顺时针转一步
• 操作三：内环逆时针转一步，外环顺时针转一步
• 内中外三个环，周期都是3步，即转3步后回到原位置

解决思路

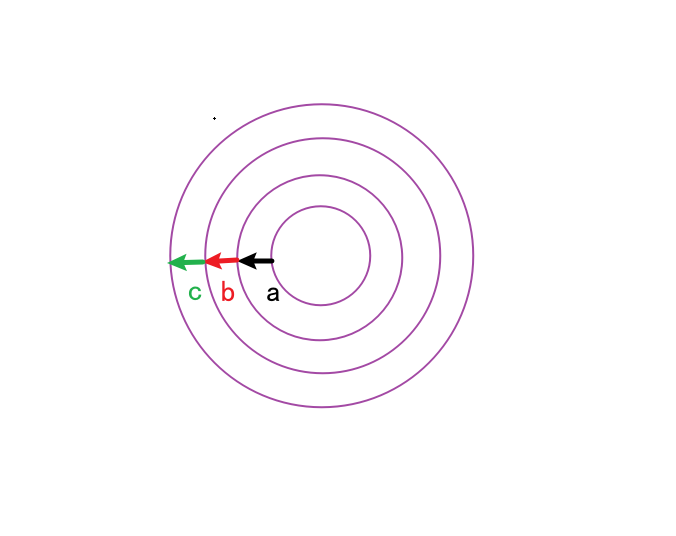
将内中外三环的指针位置分别用 a, b, c 表示，假设三个指针在给定方位对齐时，有

$$ a = 0，b = 0, c = 0 $$

根据上文规则，内中外三环的周期分别为 3，3，3，因此

• a 落在模 3 的整数环上，状态是 {0, 1, 2}
• b 落在模 3 的整数环上，状态是 {0, 1, 2}
• c 落在模 3 的整数换上，状态是 {0, 1, 2}

规定逆时针为正向，比如内环逆时针转一步，变化是

$$ a=a+1 \pmod3 $$

假设某一时刻，我们一共执行了 x 次第一类操作，y 次第二类操作，z 次第三类操作，那么按照上文的游戏规则

• 操作一：内环和中环同时逆时针转一步
• 操作二：中环逆时针转一步，外环顺时针转一步
• 操作三：内环逆时针转一步，外环顺时针转一步

可知：

• 内环的 a 一共递增了 x + z 次
• 中环的 b 一共递增了 x + y 次
• 外环的 c 一共递减了 y + z 次，即递增了 -y - z 次

因此，三个指针此时的位置分别落在

$$ a \equiv 4 + x + z \pmod 3 \\ b \equiv 0 + x + y \pmod 3 \\ c \equiv 0 - y - z \pmod 3 $$

不难看出，游戏的本质，是通过 x/y/z 次三类操作的组合，同时达成 a 模 3 为 0，b 模 3 为 0 和 c 模 3 为 0 的目标

同余方程组的求解

根据上述分析，问题等价于求下列同余方程组的解

$$ \begin{cases} 4+x+z \equiv 0 \pmod3 && ①\\ 0+x+y \equiv 0 \pmod3 && ②\\ 0-y-z \equiv 0 \pmod3 && ③\\ \end{cases} $$

下面的推导需要部分《密码学》知识，参考这篇博客：乘法逆元的原理与应用

根据 ① 得

$$ x \equiv -z-4 \pmod3 \quad ④ $$

根据 ③ 得

$$ y \equiv -z \pmod3 \qquad ⑤ $$

④ 和 ⑤ 代入 ②，得

$$ -2z - 4 \equiv 0 \pmod3 $$

因此

$$ 2z \equiv -4 \pmod3 $$

同余方程系数化 1，需要用到乘法逆元，因为 2 * 2 (mod 3) = 1，所以 2 的乘法逆元是 2

两边同乘 2，根据同余等价性，得

$$ z \equiv -8 \pmod3 $$

即

$$ z \equiv 1 \pmod3 \qquad ⑥ $$

⑥ 代入 ④ 得

$$ x \equiv 1 \pmod3 \qquad ⑦ $$

⑥ 代入 ⑤ 得

$$ y \equiv 2 \pmod3 \qquad ⑧ $$

联合 ⑥ ⑦ ⑧ ，得到

$$ \begin{cases} x \equiv 1 \pmod3 \\ y \equiv 2 \pmod3 \\ z \equiv 1 \pmod3 \\ \end{cases} $$

也就是说，所有能拧开这个罗盘的操作序列，必定符合以下规律：第一种操作数除以 3 余 1，第二种操作数除以 3 余 2，第三种操作数除以 3 余 1

因此，这个谜题的最简解法是：第一种操作拧 1 次，第二种操作 2 次，第三种 1 次

如图所示，4 步解开

测试

实战一

设三种操作分别执行 x, y, z 次，列同余方程组

$$ \begin{cases} 2+x+z \equiv 0 \pmod3 \\ 1+y \equiv 0 \pmod2 \\ 0+y+z \equiv 0 \pmod6 \\ \end{cases} $$

解得

$$ \begin{cases} x \equiv 2 \pmod{3} \\ y \equiv 1 \pmod{6} \\ z \equiv 5 \pmod{6} \end{cases} \quad \text{或} \quad \begin{cases} x \equiv 1 \pmod{3} \\ y \equiv 3 \pmod{6} \\ z \equiv 3 \pmod{6} \end{cases} \quad \text{或} \quad \begin{cases} x \equiv 0 \pmod{3} \\ y \equiv 5 \pmod{6} \\ z \equiv 1 \pmod{6} \end{cases} $$

取其中一种：

• 操作一：旋转 2 次
• 操作二：旋转 1 次
• 操作三：旋转 5 次

验证视频

实战二

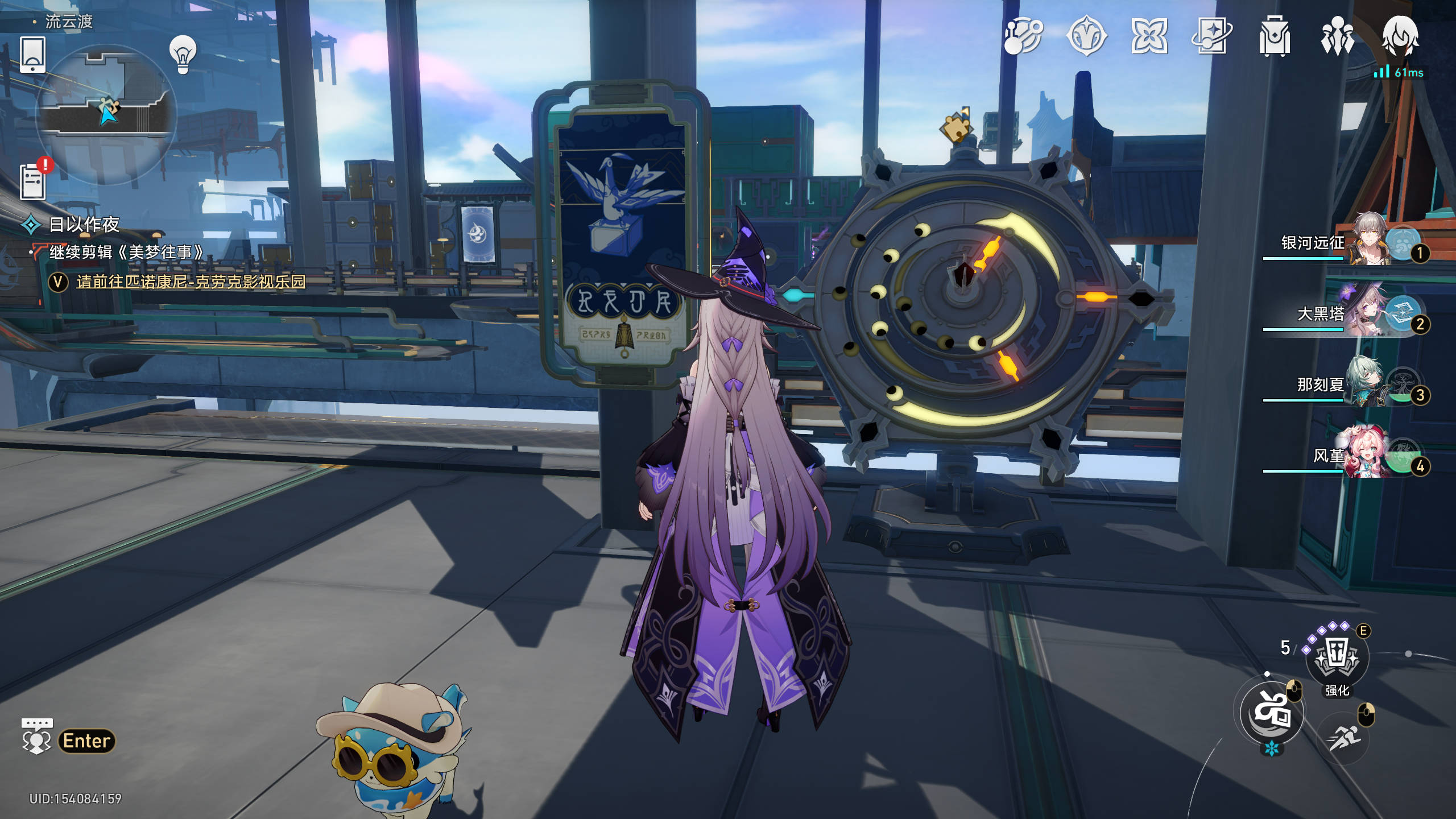
游戏信息

• 内中外三环的周期分别是 6 3 6
• 内中外三环的初值分别是 4 2 3
• 操作一：内环+1
• 操作二：中环-1，外环+1
• 操作三：内环+1，外环+1

列方程组

$$ \begin{cases} 4+x+z \equiv 0 \pmod6 \\ 2-y \equiv 0 \pmod3 \\ 3+y+z \equiv 0 \pmod6 \\ \end{cases} $$

解得

$$ \begin{cases} x \equiv 1 \pmod{6} \\ y \equiv 2 \pmod{6} \\ z \equiv 1 \pmod{6} \end{cases} \quad \text{或} \quad \begin{cases} x \equiv 4 \pmod{6} \\ y \equiv 5 \pmod{6} \\ z \equiv 4 \pmod{6} \end{cases} $$

取其一：三种操作分别旋转 1 次，2 次，1 次

验证视频

实战三

• 内中外环周期是 3 6 3
• 内中外环初值是 0 3 2
• 操作一：内环-1，中环+1
• 操作二：中环+1，外环-1
• 操作三：内环-1，外环-1

方程组

$$ \begin{cases} 0-x-z \equiv 0 \pmod3 \\ 3+x+y \equiv 0 \pmod6 \\ 2-y-z \equiv 0 \pmod3 \end{cases} $$

解得

$$ \begin{cases} x \equiv 2 \pmod6 \\ y \equiv 1 \pmod6 \\ z \equiv 1 \pmod3 \\ \end{cases} $$

取最简方案，三种操作分别旋转 2 次，1 次，1 次

验证视频

盲拧成功率与环型密码锁

盲拧成功率分析

以一个游戏的方程组通解为例：

$$ \begin{cases} x \equiv 1 \pmod3 \\ y \equiv 2 \pmod3 \\ z \equiv 1 \pmod3 \\ \end{cases} $$

可知：对这局游戏而言，无论你怎么拧，先后次序是什么样的，只要同时满足以下条件就能解开

• 第二种操作的总次数除以 3 余 2
• 第一、三种操作的总次数，除以 3 都余 1

换句话说，随机掷三个非负整数，排列成 (x, y, z)，只要它们符合上面的特性就可以解开，概率是

$$ \frac{1}{3}*\frac{1}{3}*\frac{1}{3}=\frac{1}{27} $$

可见概率是跟这个游戏对应的同余方程组的通解的模数有关，三个模数的积越大，则盲拧成功率越小，谜题难度越大
同理，也跟通解的形式数有关。通解以多种形式并列的情况，比如

$$ \begin{cases} x \equiv 2 \pmod{3} \\ y \equiv 1 \pmod{6} \\ z \equiv 5 \pmod{6} \end{cases} \quad \text{或} \quad \begin{cases} x \equiv 1 \pmod{3} \\ y \equiv 3 \pmod{6} \\ z \equiv 3 \pmod{6} \end{cases} \quad \text{或} \quad \begin{cases} x \equiv 0 \pmod{3} \\ y \equiv 5 \pmod{6} \\ z \equiv 1 \pmod{6} \end{cases} $$

这种情况，解开概率是

$$ \frac{1}{3*6*6}+\frac{1}{3*6*6}+\frac{1}{3*6*6}=\frac{1}{36} $$

环型密码锁

我们换个角度去看这个游戏的通解

$$ \begin{cases} x \equiv 1 \pmod3 \\ y \equiv 2 \pmod3 \\ z \equiv 1 \pmod3 \\ \end{cases} $$

可以发现，解谜过程等价于在转一个环型密码锁的保险箱

更具体地，就像有 3 个数字环，每个数字环长度为 3 的环型锁。盲拧这个小游戏的本质，如同我们在不知道密码的情况下，随机把它从初始状态 0 0 0 随机拧到正确状态 1 2 1

出题思路

经过上面讨论，这个转盘游戏跟环型密码锁是两种外在形式不同，但本质一样的东西

我们可以利用这点，反过来自己出题

比如说，构造一把密码锁，数字环分别是 6 3 6，正确密码是 4 1 2，那么这把锁的盲拧成功率是

$$ \frac{1}{6*3*6}=\frac{1}{108} $$

假设要自定义难度，可以按比如 ≤1/a, ≤1/b, ≤1/c, >1/c 等划分出多个难度区间，然后只要调整正确密码数和三个数字环，让上述概率分别落在对应区间就行

下面将这把“锁”转换成一局罗盘游戏

列出通解

$$ \begin{cases} x \equiv 4 \pmod6 \\ y \equiv 1 \pmod3 \\ z \equiv 2 \pmod6 \\ \end{cases} $$

构造方程组

符合这个解的方程组可以有很多。其中一个可行的是：

$$ \begin{cases} x+y \equiv 5 \pmod3 \\ x+z \equiv 6 \pmod6 \\ y-z \equiv -1 \pmod3 \\ \end{cases} $$

右边归 0，得

$$ \begin{cases} 1+x+y \equiv 0 \pmod3 \\ 0+x+z \equiv 0 \pmod6 \\ 1+y-z \equiv 0 \pmod3 \\ \end{cases} $$

将上述方程组三个常数 1 0 1 作为初值，将三个模数 3 6 3 作为三环周期，而每条方程的变量系数，对应了三种操作下每个环的转动方向和转动步长。

即，按游戏语言可描述为：

• 形状

  • 内环周期为 3，初始指针在 1
  • 中环周期为 6，初始指针在 0
  • 外环周期为 3，初始指针在 1

• 规则

  • 操作一：内环和中环同时逆时针旋转一步
  • 操作二：内环和外环同时逆时针旋转一步
  • 操作三：中环逆时针旋转一步，外环顺时针旋转一步

之后根据这些数据，构造一局游戏即可。

暴力破解法

算三个环周期的最小公倍数，以它作为密码锁每个数的周期（假设三环周期 3 2 6，那么锁上每个数字环的周期是 6）

然后把轮盘的 UI 遮住，只留三个操作按钮，想象按钮上面的不是轮盘，而是一个以 0 0 0 为起点的密码锁

我们怎么将一把锁从 0 0 0 拧到 5 5 5，就怎么按顺序试完所有按钮。把所有组合枚举一遍，能解开轮盘对应环形锁模型的，自然能解开轮盘

不过，与文章前面提到的数学解法相比，暴力破解效率较低，特别是当环的周期较大时，尝试的组合数会急剧增加。前文提到的通过同余方程组求解的方法更为高效，能直接得出最优解

总结

我们通过数学建模，给出了崩铁转盘类谜题的通用解法。不仅可以轻松解决游戏中遇到的各种难度的谜题，还能自己设计出难度可控的谜题。希望这个攻略能帮助到同玩的开拓者们，让各位探索仙舟的旅程更加顺利！