前言
根据上篇文章,牧场物语本质是这样一个系统:
用每天自动到账的有限的时间和体力资源换尽可能多的钱
其中,
物品是时间&体力与金钱价值交换的中间物,如果把物品从买入到其加工品/产品卖出看作一个闭环。那么闭环上凝聚在物品身上的每次劳动,本质上还是用时间和体力换金钱
方便起见,以国外的一款同人游戏 Rewrite: A Village Life 为例,深入钻研一下如何在此类游戏中快速赚钱
数据的收集
时间&体力系统
- 主人公 11 睡 6 起,所以每天有 17 小时自由时间;
- 实测 1 天极限可以浇 60 次水,钓 40 次鱼,捡 60 次东西,可定为 体力 120
游戏里,赚钱方式分为 4 种:
- 种地
- 钓鱼
- 养动物
- 捡东西
下面一一详细分析
种地(作物系统)

作物系统如下:
| 作物 | 成本 / 元 | 售价 / 元 | 周期 / 天 |
|---|---|---|---|
| 土豆 | 30 | 65 | 7 |
| 草莓 | 80 | 160 | 15 |
| 香草 | 20 | 40 | 5 |
| 黄瓜 | 60 | 210 | 33 |
| 卷心菜 | 100 | 240 | 18 |
种作物,忽略一劳永逸的耕地,主要成本都花在浇水和播种。换算后基本数据如下:
| 活动 | 时间 / 秒 | 体力 | 收益 / 元 |
|---|---|---|---|
| 种土豆 | 200 | 2 | 5 |
| 种草莓 | 200 | 2 | 5.3 |
| 种香草 | 200 | 2 | 4 |
| 种黄瓜 | 200 | 2 | 4.5 |
| 种卷心菜 | 200 | 2 | 7.8 |
钓鱼(钓鱼系统)

可以钓到的鱼有 3 种
| 鱼类 | 时间 / 秒 | 体力 | 收益 / 元 |
|---|---|---|---|
| 大鱼 | 3000 | 3 | 25 |
| 中鱼 | 3000 | 3 | 15 |
| 小鱼 | 3000 | 3 | 5 |
这是一项技术活,不是每次都能上钩。以我为样本统计的话,游戏中我只钓大鱼,每次成功率约 80%。假设中鱼 90%,小鱼 100% ,换算如下:
| 鱼类 | 时间 / 秒 | 体力 | 收益 / 元 |
|---|---|---|---|
| 钓大鱼 | 3000 | 3 | 20 |
| 钓中鱼 | 3000 | 3 | 13.5 |
| 钓小鱼 | 3000 | 3 | 5 |
养动物(动物系统)
动物系统很简单,只有鸡羊牛,不用饲料,放置一定天数后可稳定带来收入,其中
| 动物 | 买入价格 / 元 | 成熟时间 / 天 | 产品价格 / 元 |
|---|---|---|---|
| 鸡 | 500 | 20 | 30 |
| 羊 | 650 | 25 | 40 |
| 牛 | 800 | 30 | 50 |
换算如下:
| 动物 | 时间 / 秒 | 体力 | 收益 / 元 |
|---|---|---|---|
| 捡鸡蛋 | 300 | 2 | 30 |
| 剪羊毛 | 300 | 0 | 40 |
| 挤牛奶 | 300 | 0 | 50 |
捡东西(掉落系统)

路边的东西捡起之后,可以卖了换钱。游戏里我 4 小时内可以捡 50 次左右,换算一下:
| 物品 | 时间 / 秒 | 体力 | 收益 / 元 |
|---|---|---|---|
| 捡木材 | 300 | 2 | 5 |
| 捡石头 | 300 | 2 | 5 |
| 捡蘑菇 | 300 | 2 | 12 |
| 捡黄花 | 300 | 2 | 15 |
| 捡大蒜 | 300 | 2 | 16 |
| 捡苹果 | 300 | 2 | 20 |
游戏里所有物品(以下称为掉落)数目是有限的,而且可再生。区别是木材,石头的位置是固定的,廉价但每日可再生,而蘑菇,黄花,大蒜,苹果(以下称为稀有掉落)价高量少。就像随机出现一样,有时有,有时没有;有时多,有时少。很难按照经验判断
所以这里采用统计的方式寻找数值规律。如果有,按规律来;如果没有,用概率期望代替数目
"绝食" 4 天,等所有掉落出现再开始,一共有 4 个地点可以捡东西。截图如下

从春 5 日到春 17 日,同一位置不同天数蹲点稀有掉落。(全部截图数据看这里)
根据截图整理数据
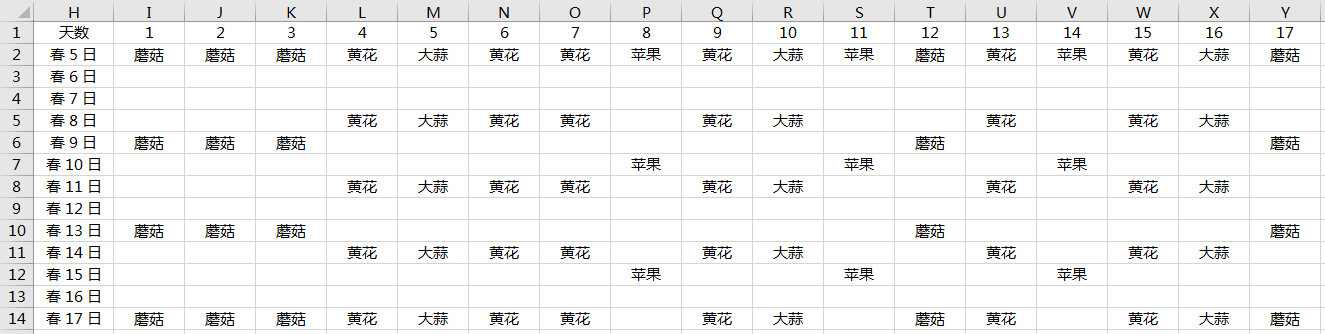
可以发现具有以下规律:
- 每个 “坑位” 出现的掉落种类是固定的(同一个坑不会出现两种掉落)
- 蘑菇每 4 天出现 1 次(准确讲是从采摘后算起 3 日重生,下同),一共 5 个坑
- 黄花每 3 天出现 1 次,一共 6 个坑
- 大蒜每 3 天出现 1 次,一共 3 个坑
- 苹果每 5 天出现 1 次,一共 3 个坑
注意到 3 天 1 掉落,4 天 1 掉落,5 天 1 掉落,最小公倍数是 60。这意味着如果每天都捡稀有掉落,那么 60 天掉落的分布就会出现周期。一个周期里一共可以稳定捡到 75 朵蘑菇,120 朵黄花,60 棵大蒜,36 个苹果,合计 4380 元,日均收入 73。而日均体力消耗 9.7,日均时间半小时。相当强悍的数值。每天只捡稀有掉落,游戏结束能带来 13140 元收入。如果再考虑普通掉落,木材数量 29,石头数量 22。每天再能带来 252 的收入,消耗体力 102,所需时间 4 个半小时。预计收入 58500 元
多说一点,通过表格可以发现如果初始状态是全满的,那么接下来所有物品的位置都是可预测的。
我们可以利用这一点。比如说 1-3 其实位于 A 地,4-7 是 B 地,8-17 是 C 地。我们会发现按照周期规律,有些天数不必跑图,比如 6,7,12,17 号全图无掉落。有些天数不必跑特定地点,比如 6,7,8,10,11,12,14,15,16 号地点 A 空空如也;而 6,7,9,10,15,16 号 B 地没有东西。注意这些细节可以帮我们少走弯路,少花时间
问题的分析
先将上面收集的数据合并,然后分别计算金钱对时间&体力的比例
| 活动 | 时间 / 秒 | 体力 | 收益 / 元 | 收益时间比 | 收益体力比 |
|---|---|---|---|---|---|
| 种土豆 | 200 | 2 | 5.0 | 0.0250 | 2.00 |
| 种草莓 | 200 | 2 | 5.3 | 0.0265 | 2.65 |
| 种香草 | 200 | 2 | 4.0 | 0.0200 | 2.00 |
| 种黄瓜 | 200 | 2 | 4.5 | 0.0225 | 2.25 |
| 卷心菜 | 200 | 2 | 7.8 | 0.0390 | 3.39 |
| 钓大鱼 | 3000 | 3 | 20 | 0.0067 | 6.67 |
| 钓中鱼 | 3000 | 3 | 13.5 | 0.0045 | 4.50 |
| 钓小鱼 | 3000 | 3 | 5 | 0.0017 | 1.67 |
| 捡鸡蛋 | 300 | 2 | 30 | 0.1000 | 15.0 |
| 剪羊毛 | 300 | 0 | 40 | 0.1333 | Inf |
| 挤牛奶 | 300 | 0 | 50 | 0.1667 | Inf |
| 捡木材 | 300 | 2 | 5 | 0.0167 | 2.50 |
| 捡石头 | 300 | 2 | 5 | 0.0167 | 2.50 |
| 捡蘑菇 | 300 | 2 | 12 | 0.0167 | 6.00 |
| 捡黄花 | 300 | 2 | 15 | 0.0167 | 7.50 |
| 捡大蒜 | 300 | 2 | 16 | 0.0167 | 8.00 |
| 捡苹果 | 300 | 2 | 20 | 0.0167 | 10.00 |
- 从数据上看,最值得做的事依次是挤牛奶,剪羊毛,捡鸡蛋,每天 15 分钟就能带来 120 元收入,而且还几乎没有体力要求,白话说就是躺着赚钱。是整个游戏最不平衡的活动
- 然后是稀有掉落。沿用上一节的分析,只捡稀有掉落,半小时 + 10 点体力 = 73 元。换算成两个比例明显高于除了养动物外的其他数据
- 如果种作物,就只种卷心菜。因为种所有作物都意味着浇水,而同样的体力,同样的时间付出下,卷心菜收益最高,一个动作下去就意味着收入加 7.8(相当于捡黄花或大蒜)
- 如果要钓鱼,就只钓大鱼。注意到钓三种鱼的成本一样,而即使考虑进概率,还是大鱼收益最高,很明显应该只钓大鱼(游戏里我也一直这么做)
问题的解决
上面的分析都只是定性的,如需精确的方案,还得靠工具
这里采用先完成再完美的策略。利用上面的分析适当简化假设,先解一个相对简单的问题;然后再将事情考虑完整
简化假设
- 时间,假设所有花在赶路上的时间(包括捡东西,浇水的移动,跑动物舍,小池塘等)每天不超过 4 小时。这样每天可用时间就是 13 小时
- 动物系统,假设 40 天后每天固定安排主角捡鸡蛋,剪羊毛,挤牛奶。因为这三件事优势明显且最早 40 天开始
- 掉落系统,假设每天固定安排主角捡所有稀有掉落。原因见上
- 作物系统,假设只种卷心菜。原因见上
- 钓鱼系统,假设只钓大鱼。原因见上
集合
- 日期:DATE /1 ... 180/
- 稀有掉落位置:PLACE /1 ... 17/
数据
- 稀有掉落价值:itemValue(i, j) /DATE(i), PLACE(j)/
变量
- 每天浇水次数: wateringTimes(i)
- 每天钓鱼次数: fishingTimes(i)
- 每天每个位置是否捡稀有掉落:isPick(i, j)
- 每天捡普通掉落次数:pickNormTimes(i)
定义如下:
- wateringTimes(i) ∈ N
- fishingTimes(i) ∈ N
- isPick(i, j) ∈ {0, 1}
- pickNormTimes(i) ∈ N
中间变量
- 每天捡稀有掉落次数:pickRareTimes(i)
- 每天捡掉落次数:pickTimes(i)
- 每天使用时间: costTime(i)
- 每天使用体力: costEnergy(i)
- 每天纯收益: money(i)
定义如下:
- pickRareTimes(i) = ∑ j isPick(i, j)
- pickTimes(i) = pickRareTimes(i) + pickNormTimes(i)
- costTime(i) = wateringTimes(i) * 200 + pickTimes(i) * 300 + fishingTimes(i) * 3000
- costEnergy(i) = wateringTimes(i) * 2 + pickTimes(i) * 2 + fishingTimes(i) * 3
- money(i) = wateringTimes(i) * 7.8 + (∑ j (isPick(i, j) * itemValue(i, j))) + pickNormTimes(i) * 5 + fishingTimes(i) * 20
目标
- 游戏结束后最大化收益: max = Σ i (money(i)) + 14850
根据 40 天后每天养动物的假设,它在剩余 140 天的收入减成本为 14850
限制条件
- 每天使用时间不超过 45900: costTime(i) <= 45900
- 每天使用体力不超过 118: costEnergy(i) <= 118
- 每天浇水次数不超过 252:wateringTimes(i) <= 252
- 根据每天养动物的假设,每天时间 13 小时减 30 分钟为 45900 秒,每天体力 120 减 2 为 118
- 浇水次数不超过 252 是因为主角只有 21*12 = 252 格田
写代码
!集合与变量
sets:
DATE/1..180/:wateringTimes, fishingTimes, pickNormTimes, pickRareTimes, pickTimes, costTime, costEnergy, money;
PLACE/1..17/;
DP(DATE,PLACE):isPick, itemValue;
endsets
!数据输入与输出
data:
itemValue = @OLE('E:\lingo\牧场物语.xlsx', 'itemValue');
@OLE('E:\lingo\牧场物语.xlsx', 'wateringTimes', 'fishingTimes', 'pickNormTimes', 'pickRareTimes', 'costTime', 'costEnergy', 'money', 'isPick') = wateringTimes, fishingTimes, pickNormTimes, pickRareTimes, costTime, costEnergy, money, isPick;
enddata
!变量定义
@for(DATE(i):@gin(wateringTimes(i)));
@for(DATE(i):@gin(fishingTimes(i)));
@for(DATE(i):@gin(pickNormTimes(i)));
@for(DP(i,j):@bin(isPick(i,j)));
@for(DATE(i):pickRareTimes(i)=@sum(PLACE(j):isPick(i,j)));
@for(DATE(i):pickTimes=pickRareTimes(i)+pickNormTimes(i));
@for(DATE(i):costTime(i)=wateringTimes(i)*200 + pickTimes(i)*300 + fishingTimes(i) * 3000);
@for(DATE(i):costEnergy(i)=wateringTimes(i)*2 + pickTimes(i)*2 + fishingTimes(i)*3);
@for(DATE(i):money(i)=wateringTimes(i)*140/18 + @sum(PLACE(j):isPick(i,j)*itemValue(i,j)) + pickNormTimes(i)*5 + fishingTimes(i)*20);
!限制条件
@for(DATE(i):costTime(i)<45900);
@for(DATE(i):costEnergy(i)<118);
@for(DATE(i):wateringTimes(i)<252);
!目标函数
MAX = @sum(DATE(i):money(i)) + 14850;跑代码
新建 excel 文件,分别输入掉落系统价格与分布数据,并指定结果输出区域,存为 'E:lingo牧场物语.xlsx'
可以点击这里下载数据表
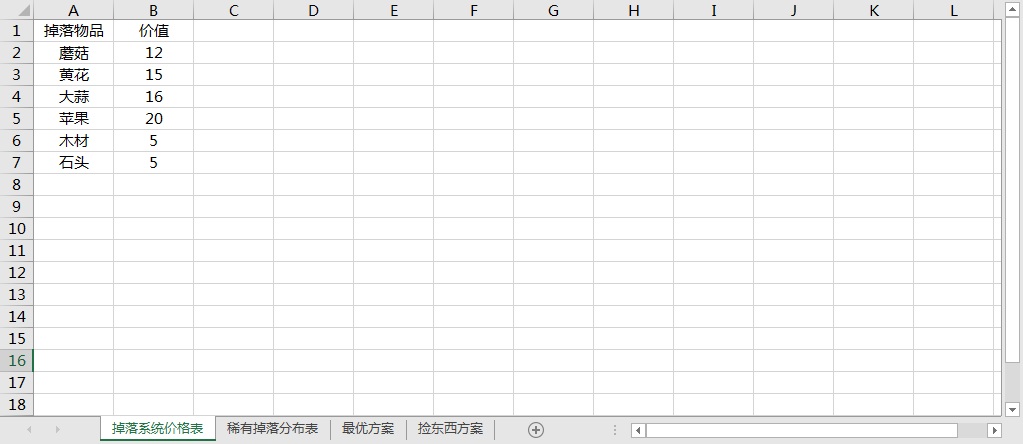
分别将 B2:B5 单元格命名为 mushroom, yellowFlower, garlic, apple
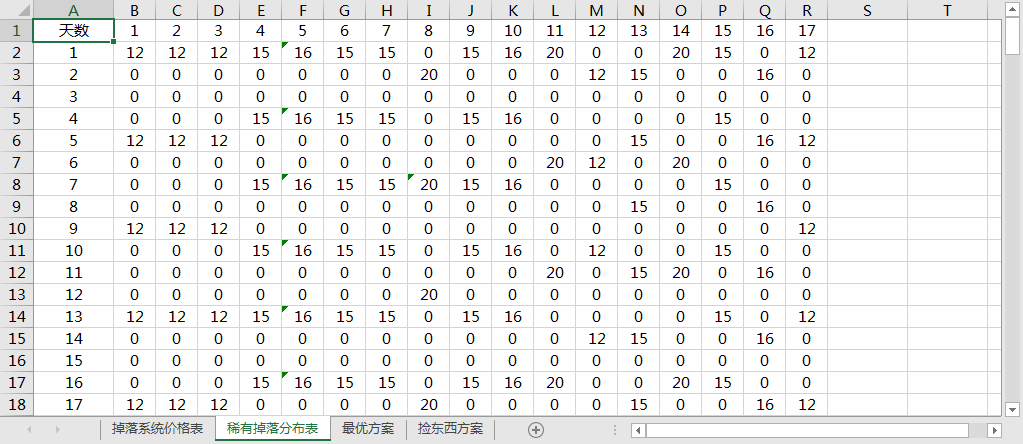
每行代表 1 天,每列代表 1 个掉落地点,单元格数据引用自第一个表的四个命名数据,并按稀有掉落生长规律每 3/4/5 天自动生成。整个数据区域命名为 itemValue,为程序提供数据输入
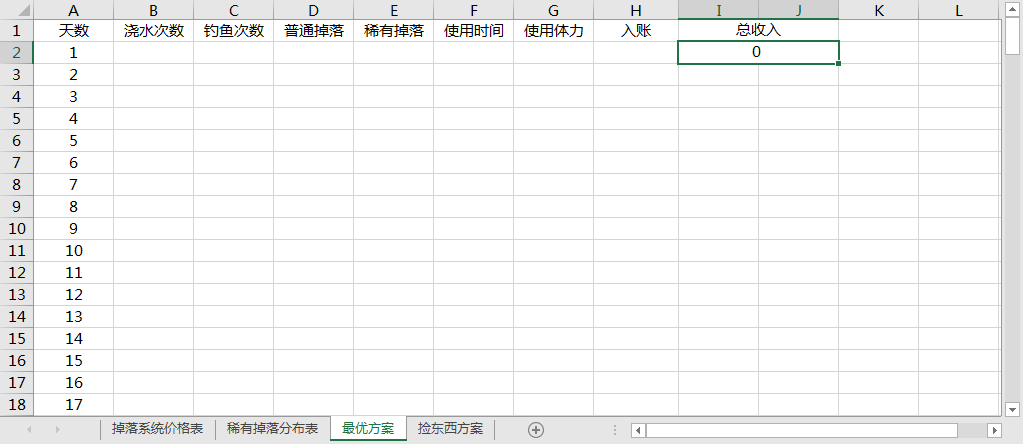
将 B, C, D, E, F, G, H 列数据行分别命名为 wateringTimes, fishingTimes, pickNormTimes, pickRareTimes, costTime, costEnergy, money,为程序准备数据输出
将 B3:R182 命名为 isPick,为程序准备数据输出
运行结果
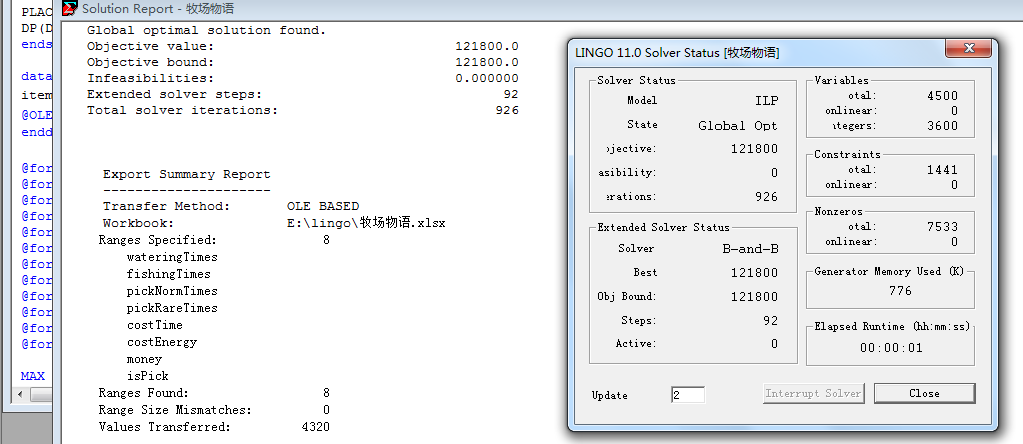
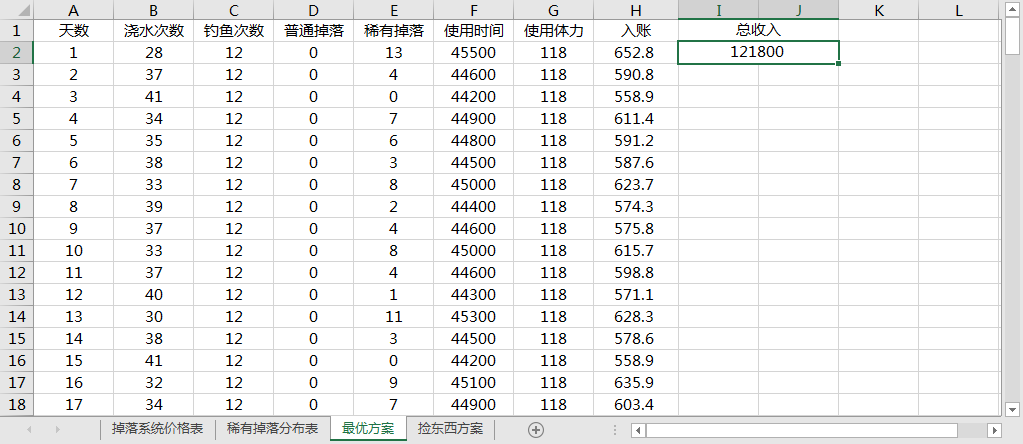
最优活动方案:
垃圾佬指南:
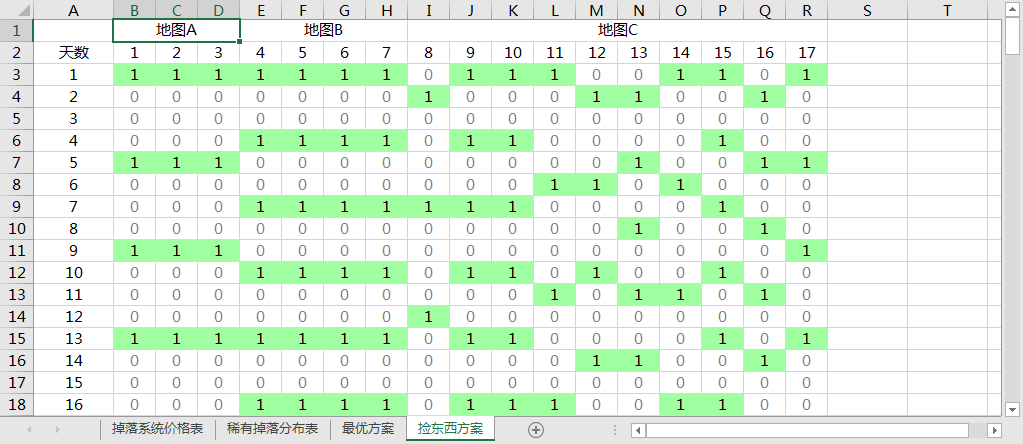
1 表示捡对应编号地点的掉落,0 表示不捡
从上表可以看出最优方案的特点
- 时间与体力相比,体力紧缺,而每天总有 10 分钟到半小时不等的时间容余
- 认为普通掉落(木材,石头)不值得捡
- 把烧时间大头安排给钓鱼活动。每天固定 12 次钓鱼,预计占用 10 小时,收益 240 元
最终收入是 12w (平均月入 2w),超出通关目标 (3w) 3 倍左右。
方案的改进
一个完整的方案终于出来了。但如果把方案付诸实践,会发现它在细节上存在问题:
- 启动资金不足
第一天就安排浇水 28 次并不现实。实际上,第 1 天只有 200 块钱,且不说土地长满杂草还没开发,就这点钱最多买 2 包种子,根本无法达成。浇水也是先要有作物的。
这个问题,可以通过预留启动天数解决。也就是说,预留一定的启动天数,攒够一定钱,等到资金足够的时候。我再以那一天为起点规划最优方案。
- 部分潜在收益被算入最终收益
问题源于作物只能在一个周期内产生收益的特点。想象一下,第 3 天浇水 41 次而第 4 天 34 次。这就意味着有部分作物必浇不到,根据游戏设定,不浇水虽然不会死,但却会延迟收成。每个作物 18 天成熟,最乐观的估计是游戏结束时所有的作物都已卖出。而实际难免会出现部分作物还没收成,凝聚在这上面的潜在收益却被我们当成实际收益
这个问题,可以通过容许一定误差解决。确实有部分收益最后不会转化为收入。最终收入减去这部分误差,给出一个范围即可。
- 播种也消耗时间体力
打个比方,1 棵卷心菜 18 天成熟,一共需要播种 1 次,浇水 18 次。播种与浇水消耗同样的时间体力。之前一直假设播种的工作忽略不计,但实际列出日程表后,这部分已经不能不算
修改潜在收益数据即可,比如之前卷心菜收益 140,平均每次浇水 140 / 18 = 7.8 元。现在加上播种,平均每次改为 140 / 19 = 7.4 元
考虑进前面的缺陷,一一改进
考虑启动资金
先算启动资金。首先,需要 41 袋种子和 3 头动物,总计 41*100 + 1950 = 6050 元,先打开游戏中实验一下

可以看出,春 10 日可以攒 3542 元并完成农田的开垦。可以认为日入 350
200 开始,日入 350 的话,游戏第 5 天可以买下所有动物。游戏第 17 天可以攒够作物启动资金
同时,前面假设 40 天后动物产生的收益数字可以更精确计算,准确说,鸡 25 天,羊 30 天,牛 35 天。收益应为 (180 - 25) * 30 + (180 - 30) * 40 + (180 - 35) * 50 - 1950 = 16350
最终收益修正
可以想象,最坏情况就是游戏结束了,地里的 41 棵作物全部没换钱。这样损失就是 41 * (140 - (-100)) = 9840。
实际游戏中,如果在剩余天数不足 18 的情况下还要播种,正常应该没人会执行。也就是说,这部分损失在实际游戏过程中很大程度可以规避。
不必改一行代码,换种说法就行。我们可以说:最大收益介于 xx-9840 和 xx 之间
考虑播种行为
根据上述,改一下收益数据即可
| 活动 | 时间 / 秒 | 体力 | 收益 / 元 |
|---|---|---|---|
| 种土豆 | 200 | 2 | 4.4 |
| 种草莓 | 200 | 2 | 5.0 |
| 种香草 | 200 | 2 | 3.3 |
| 种黄瓜 | 200 | 2 | 4.4 |
| 卷心菜 | 200 | 2 | 7.4 |
改代码
!集合与变量
sets:
!/1..180/ 改为 /1..163/;
DATE/1..163/:wateringTimes, fishingTimes, pickNormTimes, pickRareTimes, pickTimes, costTime, costEnergy, money;
PLACE/1..17/;
DP(DATE,PLACE):isPick, itemValue;
endsets
!数据输入与输出
data:
!文件名改为 牧场物语_1
itemValue = @OLE('E:\lingo\牧场物语_1.xlsx', 'itemValue');
@OLE('E:\lingo\牧场物语_1.xlsx', 'wateringTimes', 'fishingTimes', 'pickNormTimes', 'pickRareTimes', 'costTime', 'costEnergy', 'money', 'isPick') = wateringTimes, fishingTimes, pickNormTimes, pickRareTimes, costTime, costEnergy, money, isPick;
enddata
!变量定义
@for(DATE(i):@gin(wateringTimes(i)));
@for(DATE(i):@gin(fishingTimes(i)));
@for(DATE(i):@gin(pickNormTimes(i)));
@for(DP(i,j):@bin(isPick(i,j)));
@for(DATE(i):pickRareTimes(i)=@sum(PLACE(j):isPick(i,j)));
@for(DATE(i):pickTimes=pickRareTimes(i)+pickNormTimes(i));
@for(DATE(i):costTime(i)=wateringTimes(i)*200 + pickTimes(i)*300 + fishingTimes(i) * 3000);
@for(DATE(i):costEnergy(i)=wateringTimes(i)*2 + pickTimes(i)*2 + fishingTimes(i)*3);
! 140/18 改为 140/19
@for(DATE(i):money(i)=wateringTimes(i)*140/19 + @sum(PLACE(j):isPick(i,j)*itemValue(i,j)) + pickNormTimes(i)*5 + fishingTimes(i)*20);
!限制条件
@for(DATE(i):costTime(i)<45900);
@for(DATE(i):costEnergy(i)<118);
@for(DATE(i):wateringTimes(i)<252);
!目标函数
! 14850 改为 16350
MAX = @sum(DATE(i):money(i)) + 16350;solve 一下
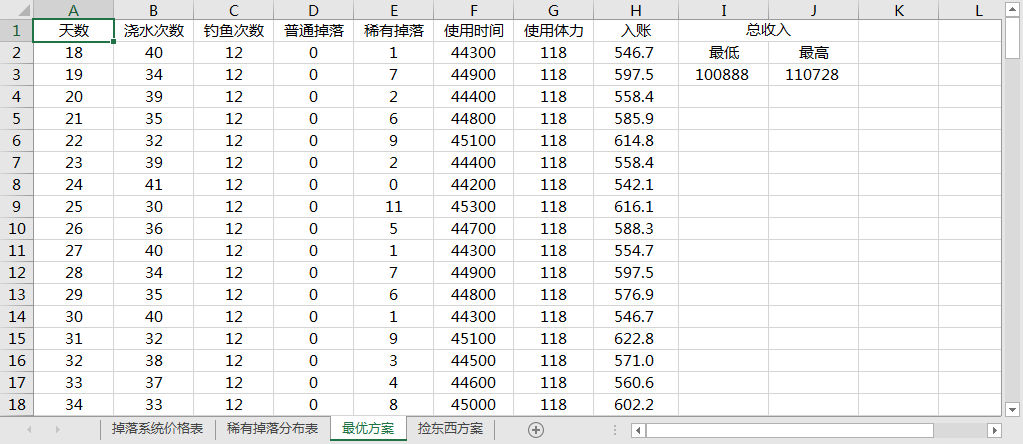
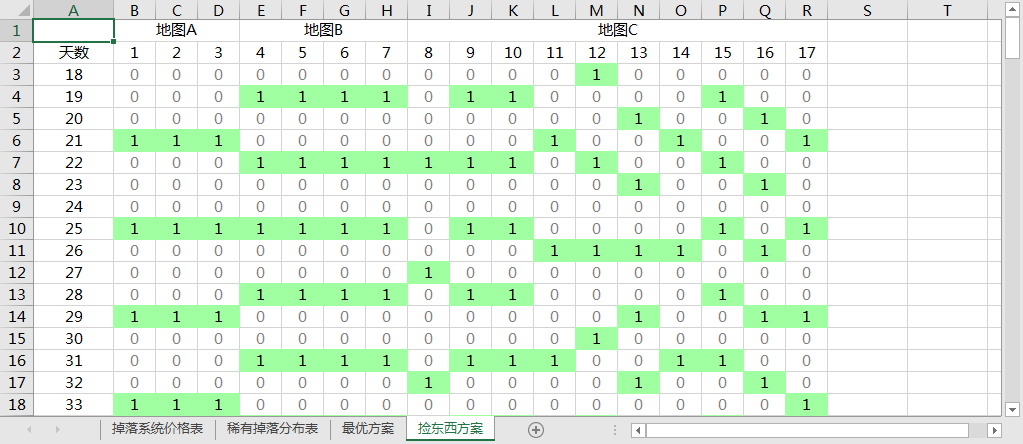
最终收入在 100888-110728 元之间,是通关目标的 3 倍以上。
Data In, Solution Out
我心中理想的规划程序应该是数据无关的,而上面的代码,还是依赖于某些数据特性以及基于这些特性才有的假设。还记得之前的先完成再完美吗?下面将去除假设,解耦代码与数据。实现这样的效果:
只需输入游戏中可直接获取的基本数据,比如
货架上的植物
| 作物 | 成本 / 元 | 售价 / 元 | 周期 / 天 |
|---|---|---|---|
| 土豆 | 30 | 65 | 7 |
农场里的动物
| 动物 | 买入价格 / 元 | 产品价格 / 元 | 成熟时间 / 天 |
|---|---|---|---|
| 鸡 | 500 | 30 | 20 |
鱼的属性
| 鱼类 | 价格 | 钩子长度 |
|---|---|---|
| 大鱼 | 25 | 30% |
就能输出解决方案
这样的好处
- 一是去除了人工分析收益与时间&体力比例然后择优的麻烦,使程序不再有基于数据特性的假设
- 二是灵活性更高。在游戏框架不变的情况下,即使你添加一个物品,调价一个商品,修改作物生长周期等等。我这边跟着改一下 excel 数据,然后程序不动,又能输出新方案。
码了半天总算完成了,下面是最终代码
!####全局参数####;
sets:
DATE/1..163/:wateringTimes, fishingTimes, pickingTimes, costTime, costEnergy, money, timeOfPlants, timeOfDrop, timeOfFishing, energyOfPlants, energyOfDrop, energyOfFishing, moneyOfPlants, moneyOfDrop, moneyOfFishing;
endsets
data:
timePerWatering, energyPerWatering, timePerFishing, energyPerFishing, timePerPicking, energyPerPicking = @OLE('E:\lingo\牧场物语_2.xlsx', 'timePerWatering', 'energyPerWatering', 'timePerFishing', 'energyPerFishing', 'timePerPicking', 'energyPerPicking');
dailyTimeLimit, dailyEnergyLimit, landLimit, animalProfit = @OLE('E:\lingo\牧场物语_2.xlsx', 'dailyTimeLimit', 'dailyEnergyLimit', 'landLimit', 'animalProfit');
enddata
!####作物系统####;
sets:
PLANTS/1..5/:plantCost, plantPrice, matureDays, plantProfit;
PP(DATE,PLANTS):plantWateringTimes;
endsets
data:
plantCost,plantPrice,matureDays = @OLE('E:\lingo\牧场物语_2.xlsx', 'plantCost', 'plantPrice', 'matureDays');
@OLE('E:\lingo\牧场物语_2.xlsx', 'plantWateringTimes') = plantWateringTimes;
enddata
@for(PP(i,j):@gin(plantWateringTimes(i,j)));
@for(DATE(i):wateringTimes(i)=@sum(PLANTS(j):plantWateringTimes(i, j)));
@for(DATE(i):wateringTimes(i)<landLimit);
@for(PLANTS(j):plantProfit(j)=(plantPrice(j) - plantCost(j)) / (1 + matureDays(j)));
@for(DATE(i):moneyOfPlants(i)=@sum(PLANTS(j):plantProfit(j)*plantWateringTimes(i,j)));
@for(DATE(i):timeOfPlants(i)=wateringTimes(i)*timePerWatering);
@for(DATE(i):energyOfPlants(i)=wateringTimes(i)*energyPerWatering);
!####掉落系统####;
sets:
PLACE/1..68/;
DP(DATE,PLACE):isPick, itemValue;
endsets
data:
itemValue = @OLE('E:\lingo\牧场物语_2.xlsx', 'itemValue');
@OLE('E:\lingo\牧场物语_2.xlsx', 'isPick') = isPick;
enddata
@for(DP(i,j):@bin(isPick(i,j)));
@for(DATE(i):pickingTimes(i)=@sum(PLACE(j):isPick(i,j)));
@for(DATE(i):moneyOfDrop(i)=@sum(PLACE(j):isPick(i,j)*itemValue(i,j)));
@for(DATE(i):timeOfDrop(i)=pickingTimes(i)*timePerPicking);
@for(DATE(i):energyOfDrop(i)=pickingTimes(i)*energyPerPicking);
!####钓鱼系统####;
sets:
FISH /1..3/: fishPrice, successRate;
DF(DATE,FISH):fishTimes;
endsets
data:
fishPrice, successRate = @OLE('E:\lingo\牧场物语_2.xlsx', 'fishPrice', 'successRate');
@OLE('E:\lingo\牧场物语_2.xlsx', 'fishTimes') = fishTimes;
enddata
@for(DF(i,j):@gin(fishTimes(i,j)));
@for(DATE(i):fishingTimes(i)=@sum(FISH(j):fishTimes(i,j)));
@for(DATE(i):moneyOfFishing(i)=@sum(FISH(j):fishPrice(j)*fishTimes(i,j)*successRate(j)));
@for(DATE(i):timeOfFishing(i)=fishingTimes(i)*timePerFishing);
@for(DATE(i):energyOfFishing(i)=fishingTimes(i)*energyPerFishing);
!####主程序####;
data:
@OLE('E:\lingo\牧场物语_2.xlsx', 'wateringTimes', 'fishingTimes', 'pickingTimes', 'costTime', 'costEnergy', 'money') = wateringTimes, fishingTimes, pickingTimes, costTime, costEnergy, money;
enddata
@for(DATE(i):costTime(i)=timeOfPlants(i) + timeOfDrop(i) + timeOfFishing(i));
@for(DATE(i):costEnergy(i)=energyOfPlants(i) + energyOfDrop(i) + energyOfFishing(i));
@for(DATE(i):money(i)=moneyOfPlants(i) + moneyOfDrop(i) + moneyOfFishing(i));
@for(DATE(i):costTime(i)<dailyTimeLimit);
@for(DATE(i):costEnergy(i)<dailyEnergyLimit);
MAX = @sum(DATE(i):money(i)) + animalProfit;
相应数据表如下(点这里下载):
全局单元格命名
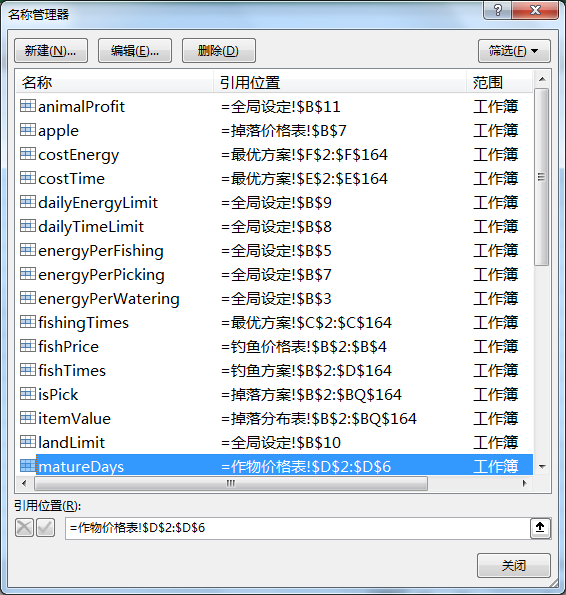
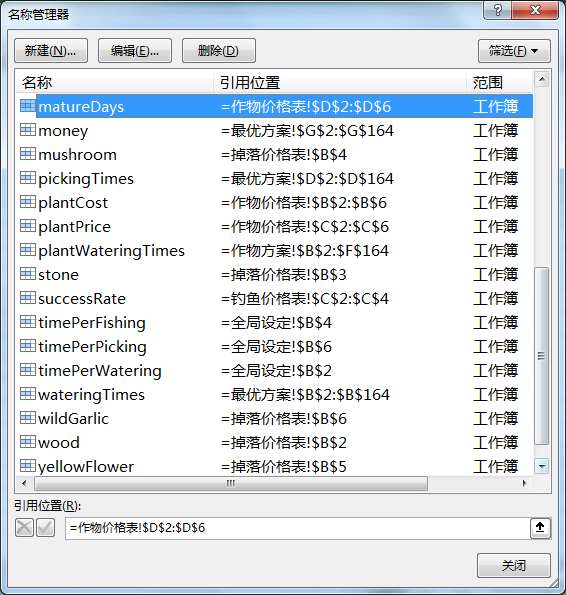
全局设定表
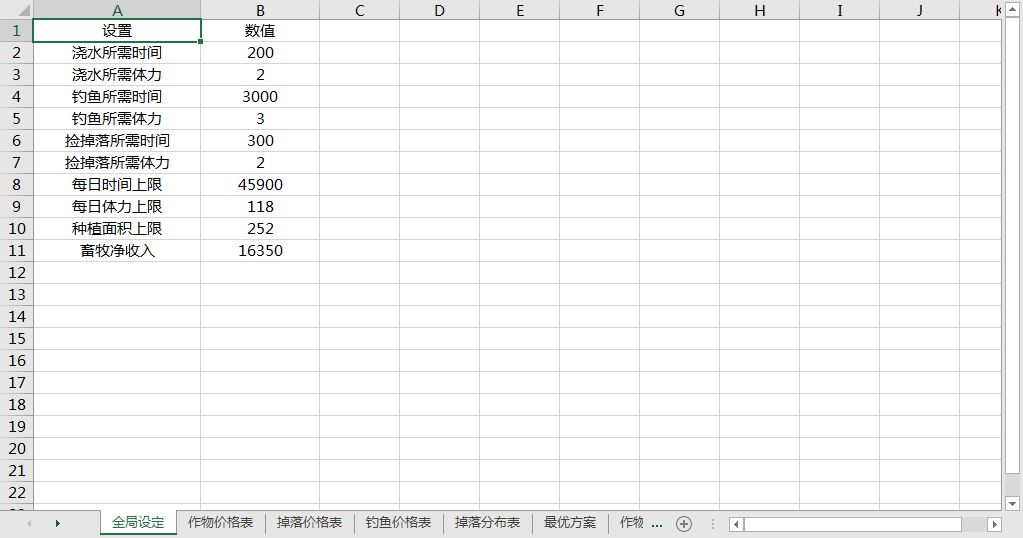
作物价格表
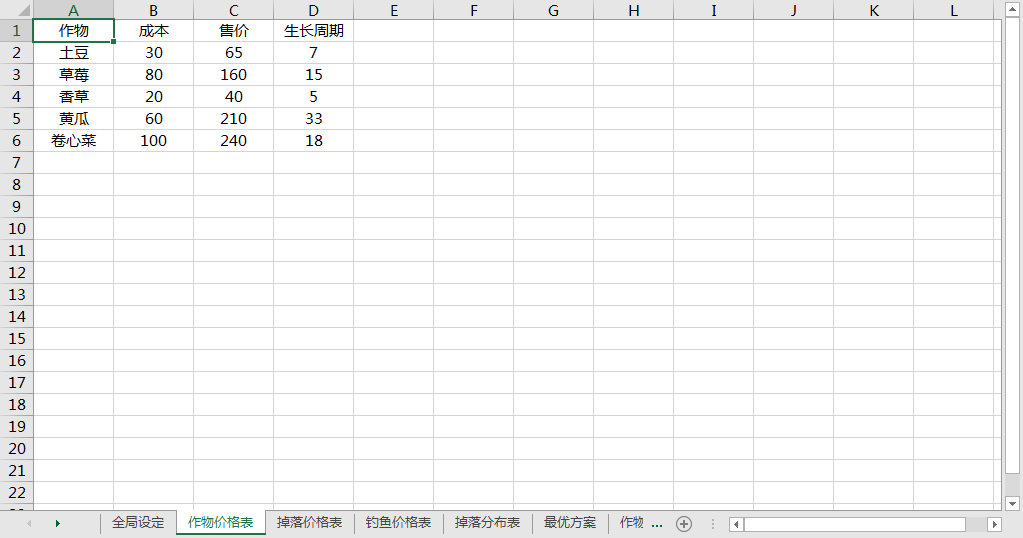
掉落价格表
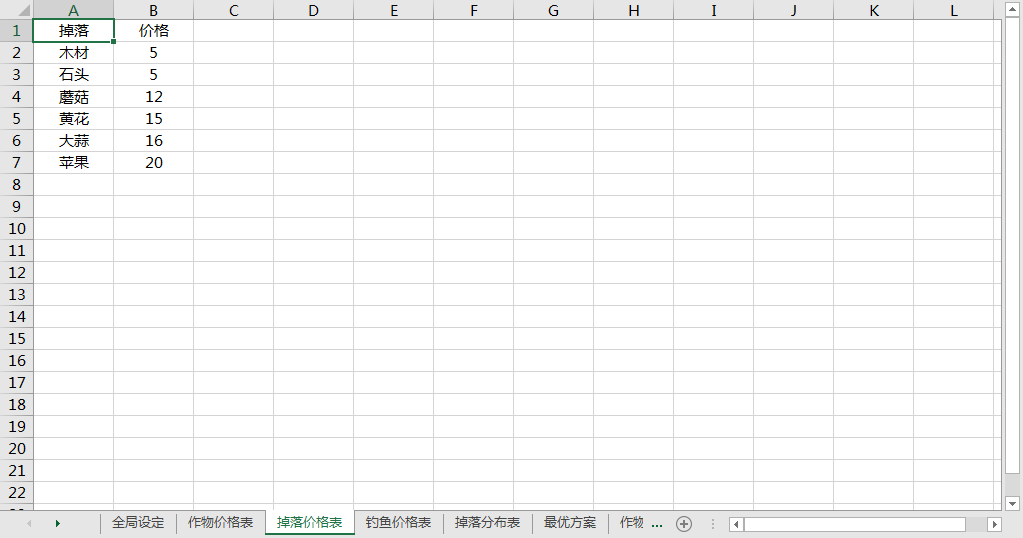
钓鱼价格表
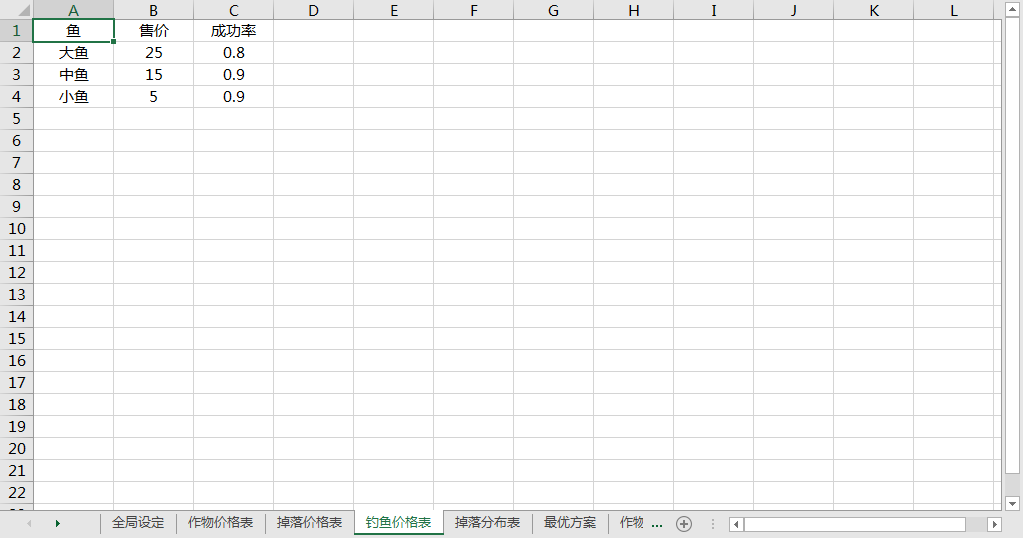
掉落分布表
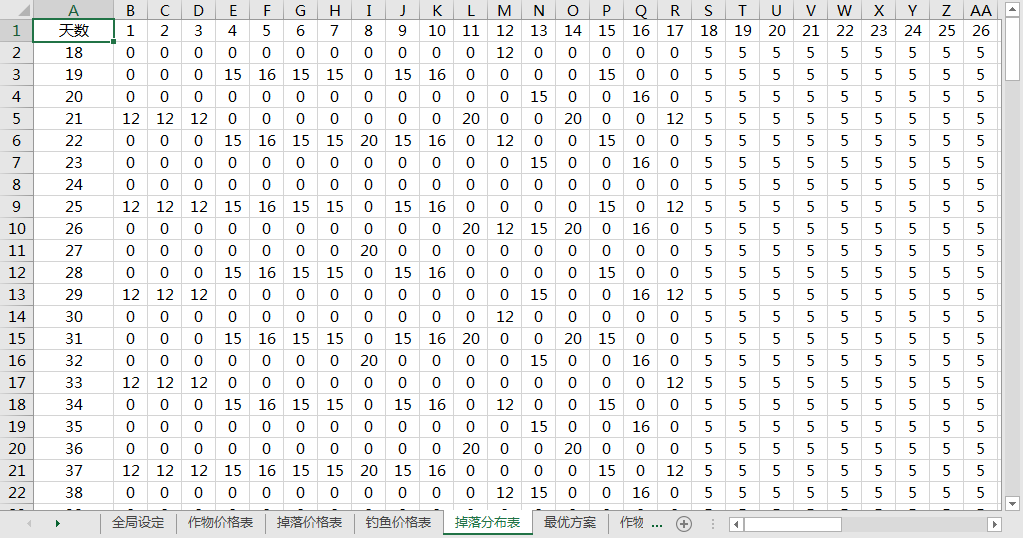
最优方案
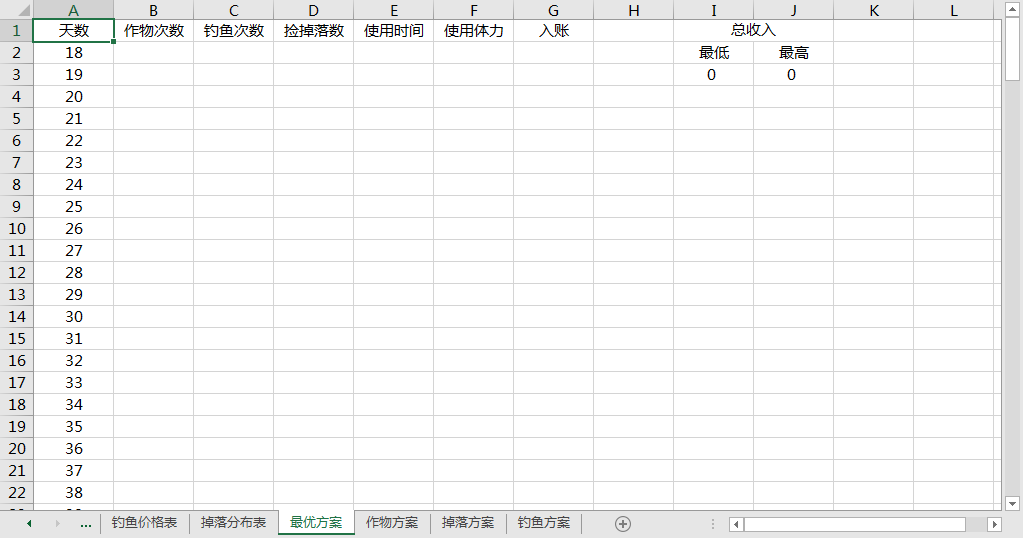
作物方案
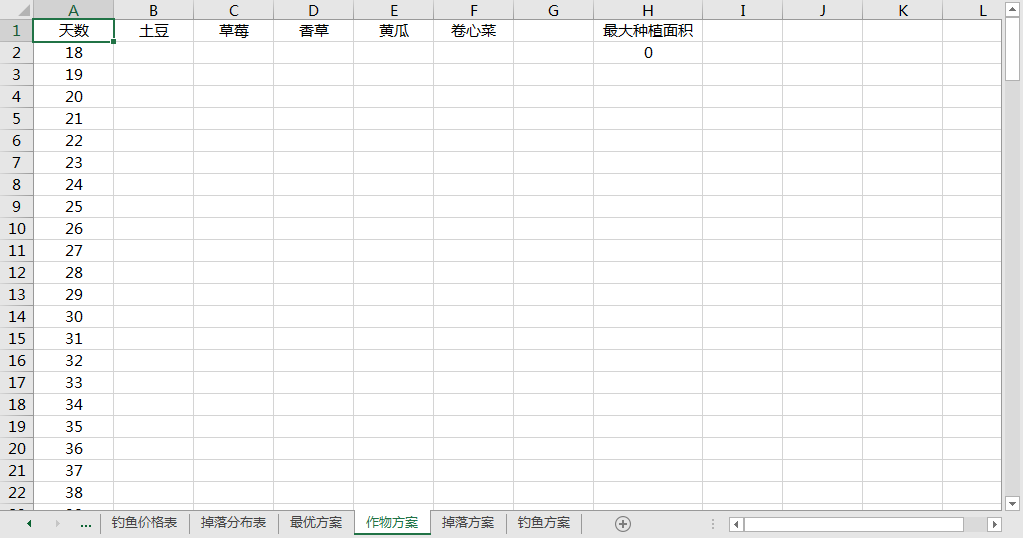
掉落方案
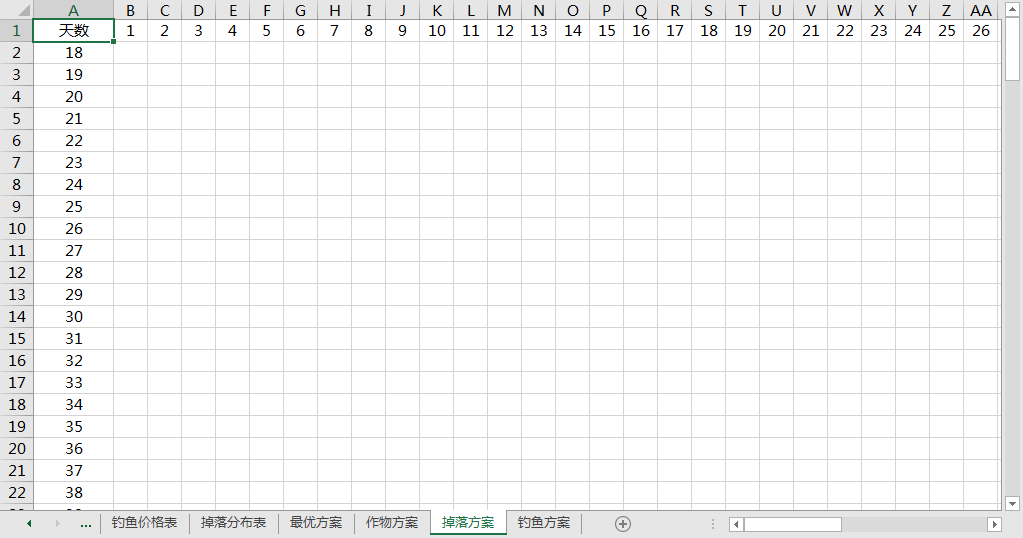
钓鱼方案
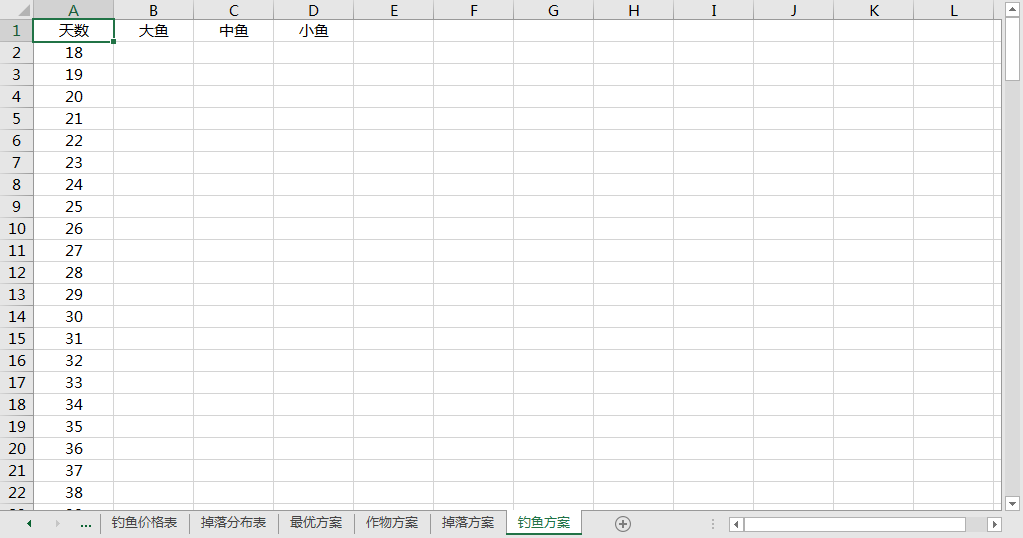
最优方案的生成
点击 solve,生成最优方案如下:
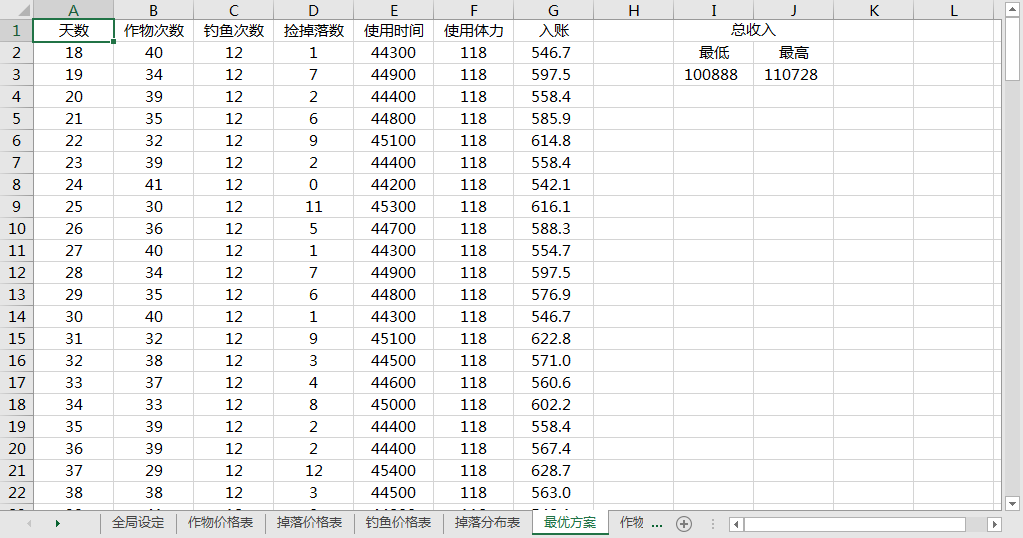
总收入给出范围,是考虑到部分潜在收益不一定转化为实际收益(比如扣除游戏结束时还没收成的蔬菜)

行代表天,列代表作物,数字 (比如 F2 = 40) 代表第 18 天卷心菜地播种+浇水次数应达到 40 次
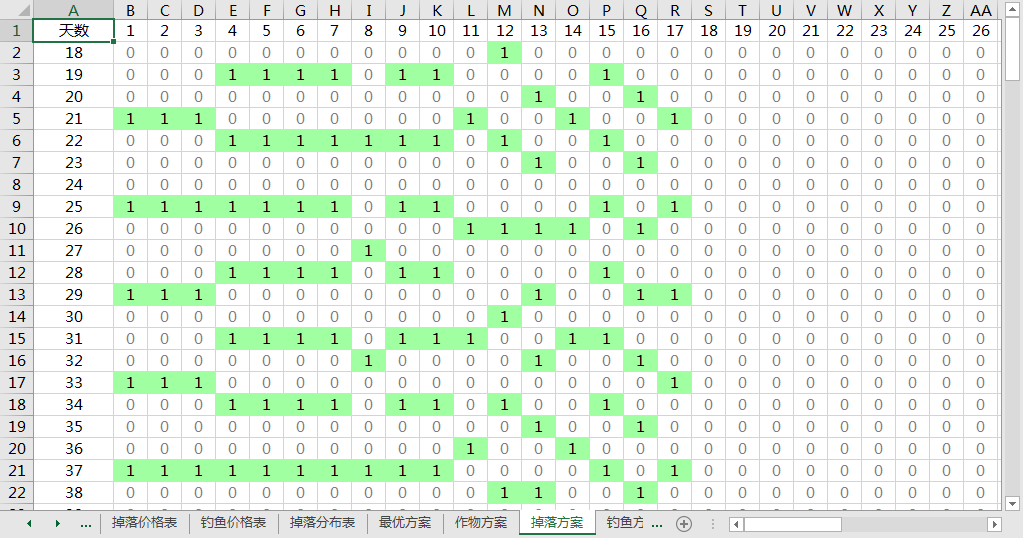
行为天数,列为掉落地点编号。1 表示捡对应位置的掉落,0 表示不捡
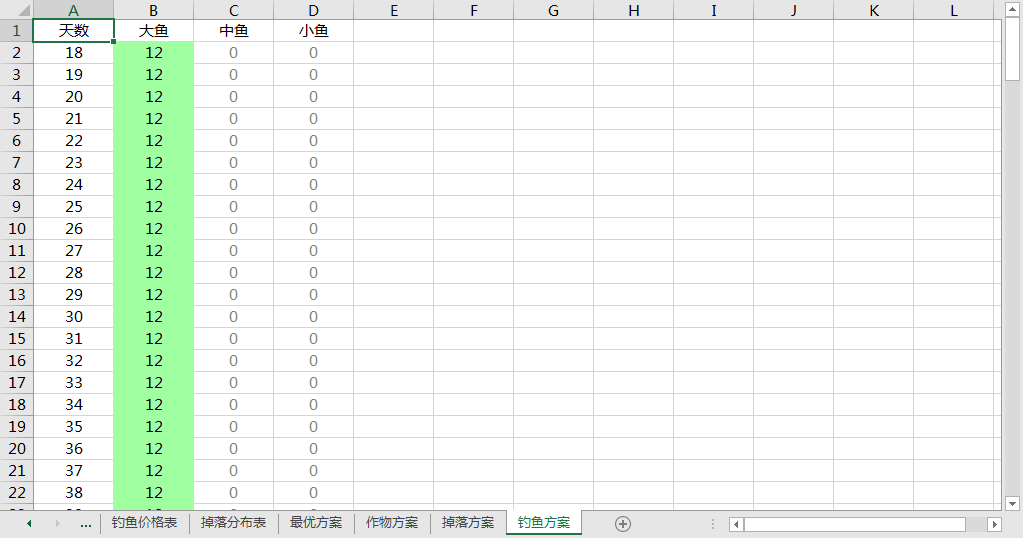
大功告成!虽然现在看上去最优方案跟之前一样,但是不同在于之前是依赖于各种数据和假设的,而现在是完全实现数据与程序解耦,不依赖于各种假设。如果游戏出了新版本,为了调整难度改了体力参数,时间参数,增加了商品种类,调整作物成熟周期 ...... 我只要改一下数据库,然后程序不变,就又能生成新方案。
比如说
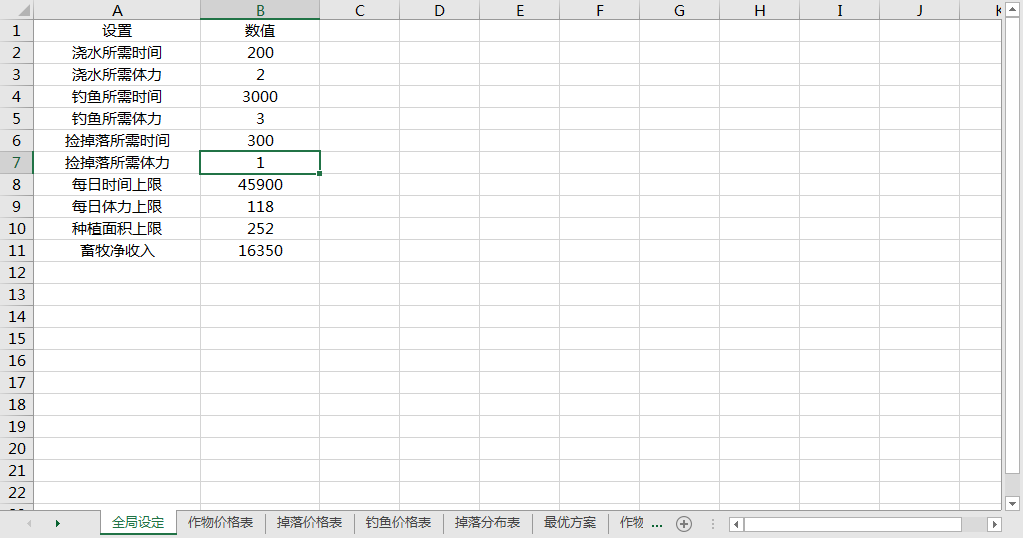
捡掉落的体力 2 => 1
方案就变成

掉落数上去了。总收入也明显上升,大约 8000 ~ 10000 左右
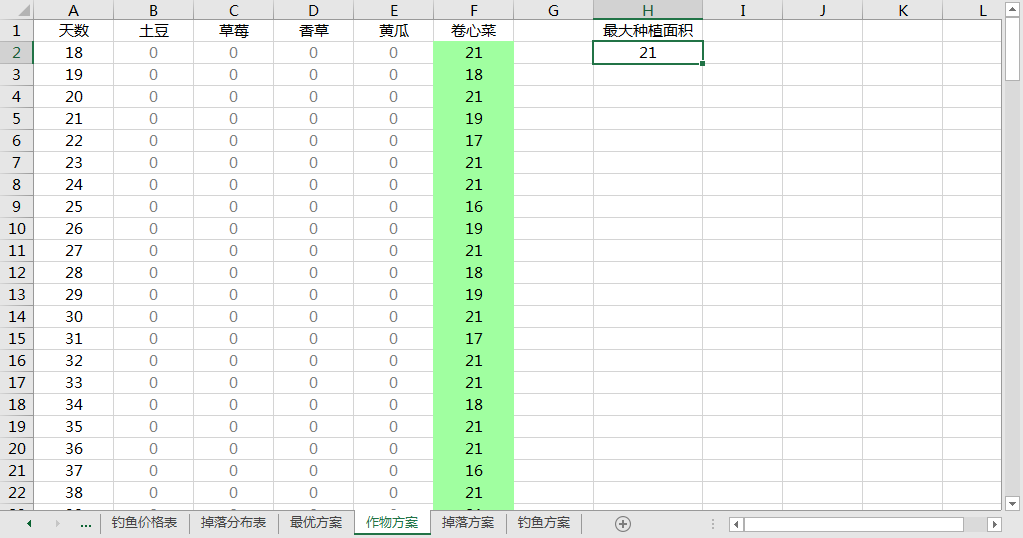
所需农田数目也从 41 降为 21
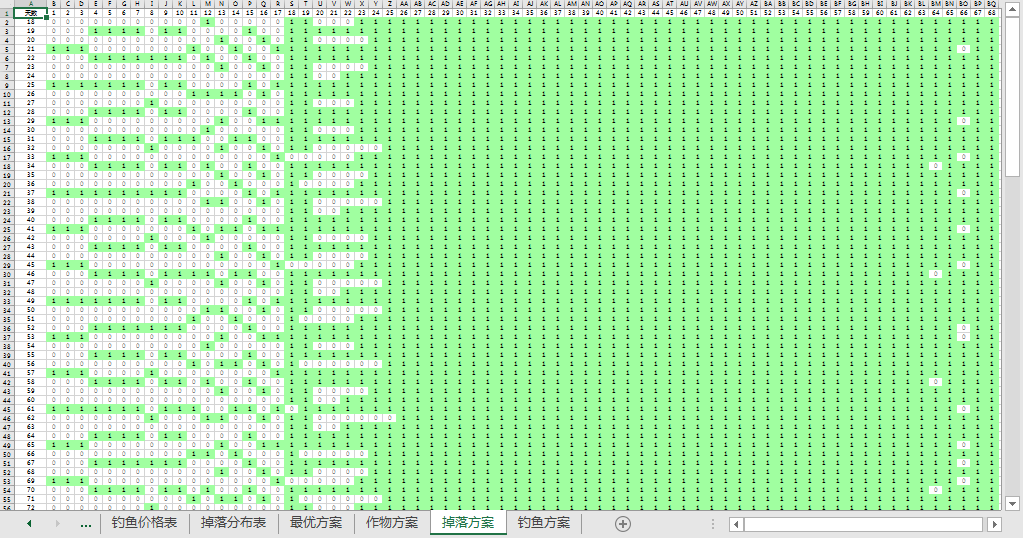
同时这一版本需要满地图跑掉落(垃圾佬的胜利)
ps: 这样一改,平衡性似乎好多了
总结改进
上面的方案实际玩游戏时没有再发现问题,确实能够按计划稳定地攒钱。非要挑毛病的话,就是过程太枯燥了。主要是钓鱼, 1 天钓 12 次。我的速度 1 分钟钓 3 条鱼,这样 1 天花在钓鱼上 4 分钟,加上其它所有活动每天都要 5 分钟以上。 1 个小时最多推进 12 天。很快就会发现游戏进展太慢
问题根源在于代码没有考虑现实时间成本这一变量。作为玩家的我们玩游戏也是需要时间和精力的,如果高效赚钱的代价是长时间的刷刷刷,恐怕也很难给屏幕外的人带来笑容
解决这个问题,只需在所有活动上添加现实时间成本这一变量。
- 比如说钓鱼,时间成本 3000,体力成本 3,实测游戏外平均时间 20s,那么现实时间就是 20
- 比如说浇水,时间成本 200,体力成本 2,平均每次 1.5s,那么现实时间就是 1.5
- ......
然后,将现实时间成本累加起来,加上负系数,给总收益一个 debuff
MAX = totalMoney - penalty * costRealTime解一下就行了。
除此之外,还可以编写游戏脚本,封装一些日常活动,然后把方案拷贝进去,让游戏过程自动化。(每天,你只要告诉我该干什么,我就按照顺序调用封装的脚本片段依次完成指定任务)
又给自己挖了个坑,有空再填吧
暂无评论