前言
学完图像处理后,自己想写这样一个程序:
输入一张图,输出此图的一笔画方案,并将路线用动态图方式展示
比如说:
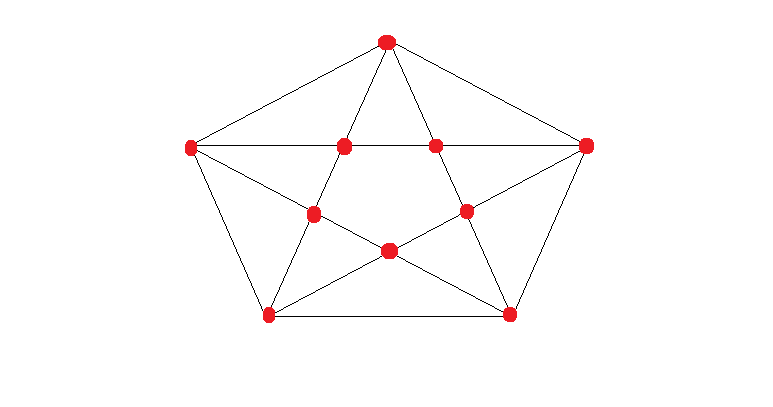
输入:
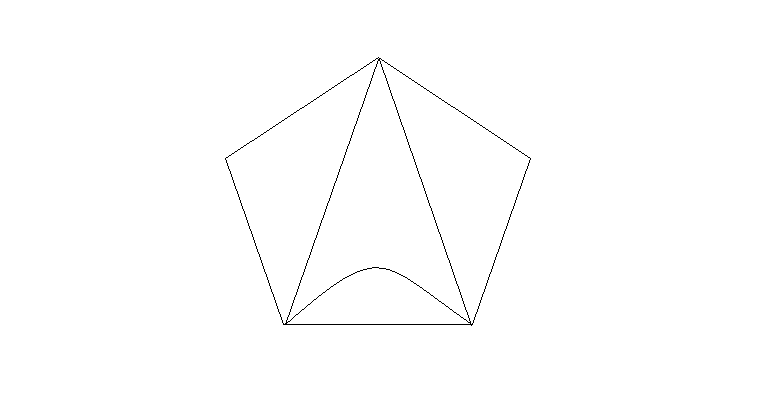
输出:

一. 思路
- 首先,对于输入的图像,可以先进行特征提取,把图像数据转化为数学模型(矩阵)表达。
- 然后,根据矩阵计算该图的一笔画解。
- 最后,将解转化为图像表达。
计算机毕竟不是人类,虽然我们脑海中的计划没问题,但是具体到实现方式上还是涉及很多边边角角的细节。
首先,提取原图的所有点元素集合和边元素集合:

然后,两者分别按连通域拆分成多张子图:









最后,一张一笔画动态图,可通过这 13 张分开图像的合理排列,逐步叠加生成。
二. 问题与解决
将实践上的主要困难记录如下:
1. 一张图有可能一笔画,也有可能不能一笔画。不能一笔画的时候怎么处理?
一笔画问题中,是否有解与图中奇点数目有关。所谓奇点,就是那些邻接的边数为奇数的点。分三种情况
- 没有奇点:说明此图可以一笔画
- 一个奇点:说明此图可以一笔画,但是得选对起点,起点就是这个唯一的奇点
- 两个奇点或以上:此图不能一笔画
注意到第二步维护一个邻接矩阵的时候,我们就可以得到图中的奇点数,所以在这一步进行处理。
如果奇点数小于等于 1,继续;否则提示无一笔解,退出。
2. 如何从一张图中提取所有点&边结构?
首先二值化,提取图像脉络图,得到预处理图 g
点的获取:用点检测算法提取所有点,按连通域分开,得到每个点
边的获取:将所有的点膨胀,用它们腐蚀 g,把原先一个连通图分割为多个连通子图,每个子图就是一条边



3. 如何存储一个邻接矩阵(获取图中的点边关系)?
用连通域
比如上面 5 张点图(设为 a1, a2, ..., a5) 和 8 张边图(b1, b2, ..., b8),做一下笛卡尔积,两两组合
然后每张合成图算一下连通度。
连通度为 1,说明该点与该边存在邻接关系;否则,说明该点该边不存在邻接关系
4. 如何从邻接矩阵计算该矩阵所代表图的一笔画序列?
关于这个问题,《离散数学》图论有一节欧拉算法
要理解这个算法,首先要了解桥的概念
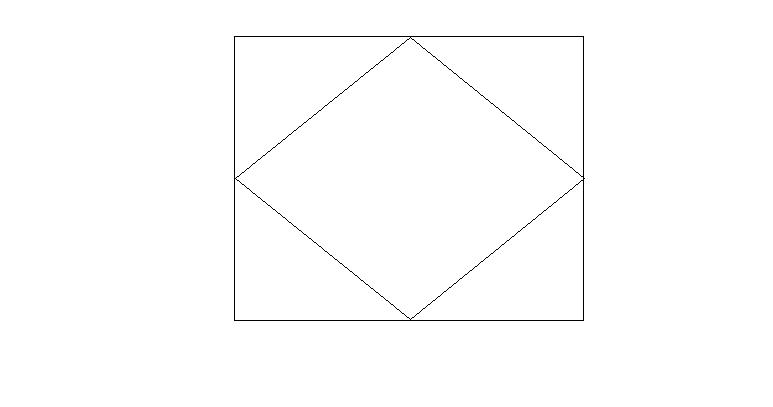
桥的概念,指图中这样一条边,删除这条边会使原图分成两半。可以通过下图直观理解
两个五角星中间有三条边连接,这三条边都不是桥,因为切断之后两边保持联系
但是三条边删除任意两条,剩下的一边是桥。因为切断之后就从一个整体变成两部分。两边相互无法联系
这是我从这个项目写的另一篇文章 桥检测算法,可以检测一张图中的桥。只是这里知道邻接矩阵的情况下没有必要用它。
然后是欧拉算法
从第一点出发,选择一条非桥的边。走过这条边,然后将它从图删除。从抵达点继续出发,重复前面的过程,直到删完图中所有边。
流程并不复杂,但将书上的理论转化为代码实际困难的是下一个问题
5. 输入一个邻接矩阵,如何判断任意一条边是否为 “桥”?
这是项目最后的困难。首先凭我之前经验是搞不定的,后来查阅资料找到一本书,查到了拉普拉斯矩阵这一概念。它有一个很好的特性,刚好能解决问题
拉普拉斯矩阵,特征值中0出现的次数就是图连通区域的个数
于是,删除该边,得到新的邻接矩阵,统计一下对应拉普拉斯矩阵特征值 0 的个数就行
小于等于 1,即少了此边连通区域还是 1 个,说明非桥。否则,此边是桥
所有的 critical point 打通了,现在就是组合 api 将项目实现
三. 实现
根据思路一开始提到的 3 点,分三个模块编写代码将各自的逻辑一一实现。每个模块都是可以独立完成任务的小工具。
- 拆图模块:输入一张图像,输出该图的邻接矩阵。并抽取离散的边帧,点帧
- 排序模块:输入一个邻接矩阵,输出该矩阵的一笔画序列(序列数组)
- 合成模块:输入边帧,点帧和序列数组,按指定的顺序叠加动态图
拆图模块:输入一张图像,输出该图的邻接矩阵。并抽取离散的边帧,点帧
g2m.m
%% 获取一张图像的邻接矩阵,边标号矩阵,散边图像与散点图像
%% 输入:一张图像 f 与点检测规模 scale
%% 输出:该图的邻接矩阵 gm,边索引矩阵 emap,散边图像 elabel 与散点图像 plabel
%% 注:点检测规模可不填,默认为10,当运行出错时赋一个较大的数可解决。
function [gm emap elabel plabel]=g2m(f,scale)
if nargin==1
scale=10;
end
g=f;
g=im2bw(g);
g=~g;
h=bwmorph(g,'thin',inf); %提取图像脉络
model=zeros(size(g));
points=catch_point(f); % 用catch_point函数检测输入图像的红点
if isempty(points) %如果没红点,手工输入图像的点
imshow(f);
points=ginput;
points=round(points);
close all;
end
for i=1:length(points(:))/2
model(points(i,2),points(i,1))=1; %model为细点图像
end
se= strel('disk',scale); %利用半径为5的圆盘进行点膨胀
fse=imdilate(model,se); %fse为粗点图像
plabel=fse;
elabel=h.*~fse; %elabel为去点的散边图
[p pnum]=bwlabel(fse);
[e enum]=bwlabel(elabel);
% figure,imshow(p);
% figure,imshow(e);
point={}; %维护点元素元胞
for i=1:pnum
p2=p;
p2(p2~=i)=0;
point{i}=p2;
end
edge={}; %维护边元素元胞
for i=1:enum
e2=e;
e2(e2~=i)=0;
edge{i}=e2;
end
gm=zeros(pnum); %初始化邻接矩阵
emap=[]; %初始化边索引矩阵
temp={};
for i=1:enum %分析每一条边与所有点的邻接情况,维护邻接矩阵
link=[];
[~,num1]=bwlabel(edge{i});
for j=1:pnum
temp{j}=edge{i}+point{j};
% figure,imshow(temp{j});
[~,num2]=bwlabel(temp{j});
if num1==num2 %如果加点前后连通域个数不变,将点号计入link数组
link=[link j];
end
end
if size(link,2)==1 %环情形把j点维护为与i点相同
link(2)=link(1);
gm(link(2),link(1))=gm(link(2),link(1))+1;
emap(link(1),link(2),gm(link(1),link(2)))=i; %维护边索引矩阵
emap(link(2),link(1),gm(link(1),link(2)))=i;
else
gm(link(1),link(2))=gm(link(1),link(2))+1; %维护邻接矩阵
gm(link(2),link(1))=gm(link(2),link(1))+1;
emap(link(1),link(2),gm(link(1),link(2)))=i; %维护边索引矩阵
emap(link(2),link(1),gm(link(1),link(2)))=i;
end
end
end排序模块:输入一个邻接矩阵,输出该矩阵的一笔画序列(边序数组)
m2seq.m
%% 根据一个邻接矩阵及边标号矩阵用算法算出一笔画边序列
%% 输入:一个邻接矩阵gm及对应的边索引矩阵emap
%% 输出:边点序列
function seq=m2seq(gm,emap)
i=1; %因是欧拉回路,故任选第一点为起点
pnum=length(gm); %获取点数
vis=zeros(1,pnum); %点访问数组
seq=[];
while sum(gm(:))~=0 %重复以下步骤直到邻接矩阵为空(无边可取)
if vis(i)==0; %如当前访问点未写入序列,将该点写入序列并标记“已写入”
seq=[seq -i];
vis(i)=1;
end
pana=[]; %pana数组存放对一个点所连各边的性质分析
for j=1:pnum
pana(j)=1-is_bridge(gm,i,j);
end
x=find(pana==1); %x代表非桥边的集合
y=find(pana==0); %y代表桥的集合
if ~isempty(x) %优先走非桥的边
x=x(1);
seq=[seq emap(i,x,gm(i,x))];
gm(i,x)=gm(i,x)-1;
gm(x,i)=gm(x,i)-1;
i=x;
elseif ~isempty(y) %无非桥的边时只能走桥
y=y(1);
seq=[seq emap(i,y,gm(i,y))];
gm(i,y)=gm(i,y)-1;
gm(y,i)=gm(y,i)-1;
i=y;
else %无路可走,说明不能一笔画,邻接矩阵不可能为空,强制跳出
break;
end
end
end合成模块:输入静态帧和序列数组,按指定的顺序叠加动态图
seq2gif.m
%% 根据散边图与散点图用顺序数组组织成gif动态图
%% 输入:散边图像elabel,散点图像plabel,以及顺序数组seq
%% 输出:一张“一笔.gif”图像
%% 第四参数可不管,若输入,可控制动态图速度,供调试用
function seq2gif(elabel,plabel,seq,speed)
[l2,~]=bwlabel(elabel); %为散边图标记连通域
[l4,~]=bwlabel(plabel); %为散点图标记连通域
stepall=length(seq);
frame={}; %帧图元胞
for i=1:stepall
if seq(i)<0 %负序列元素代表取点
seq(i)=-seq(i);
l=l4;
else %正序列元素代表取边
l=l2;
end
l(l~=seq(i))=0;
if i==1
l3=l;
else
l3=l3+l;
end
frame{i}=l3;
% picname=[num2str(i) '.png'];
% imwrite(l3,picname); %此两行按序生成多帧gif过程图像*.png
end
if nargin<4
speed=0.2;
end
for i=1:stepall %把多张图叠加为gif
if i==1
imwrite(~frame{i},'一笔.gif','gif','Loopcount',inf,'DelayTime',speed);
else
imwrite(~frame{i},'一笔.gif','gif','WriteMode','append','DelayTime',speed);
end;
end
end然后编写库函数,为上级调用提供工具
catch_point.m
%% 获取一张图像的红点坐标
%% 输入:RGB图片矩阵f
%% 输出:所有红点(红色区域)中心坐标
function point=catch_point(f)
h=zeros(size(f,1),size(f,2));
h(f(:,:,1)>f(:,:,2)+f(:,:,3)+100)=1; %搜索所有红点
[l num]=bwlabel(h); %统计所有红点中心,计入point数组
stats=regionprops(l);
point=[];
for i=1:num
point=[point;round(stats(i).Centroid)];
end
endis_bridge.m
%% 输入:邻接矩阵与其某边的两点序号 输出:如果此边不存在,返回2
%% 如果此边是桥,返回1,如果此边非桥,返回0
function judge=is_bridge(a,i,j)
if a(i,j)==0
judge=2;
else
oparts=pcounts(a);
a2=a;
a2(i,j)=a2(i,j)-1;
a2(j,i)=a2(j,i)-1;
aparts=pcounts(a2);
if aparts==oparts
judge=0;
else
judge=1;
end
endpcounts.m
%% 输入:邻接矩阵
%% 输出:连通分支数
%% 注:第二输入意为孤立点不记为连通分支,
function parts=pcounts(A,x)
D=diag(sum(A));
single=length(find(sum(A)==0));
L=D-A; %求解原图的拉普拉斯矩阵
n=eig(L);
parts=length(find(n<1e-10)); %计数拉普拉斯矩阵0特征值个数
if nargin==2
parts=parts-single;
end
end最后给入口函数
main.m
f=imread('五角星.png');
[gm emap el pl]=g2m(f,10); %获取图像邻接矩阵,边索引矩阵及散边图像(R10圆盘蚀点)
seq=m2seq(gm,emap); %根据前两个矩阵计算一笔画边序列
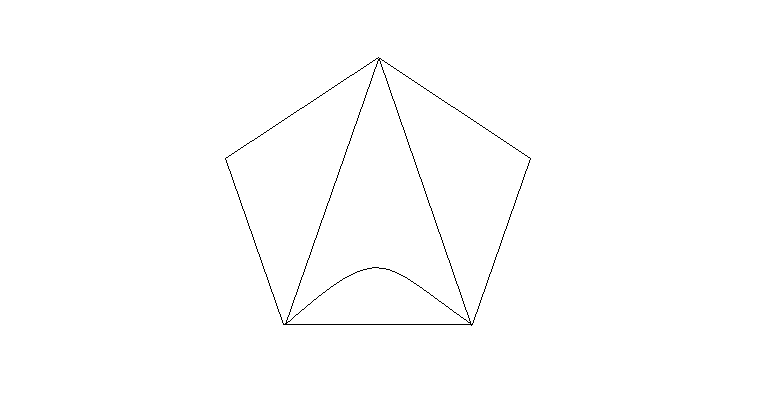
seq2gif(el,pl,seq); %根据后两张图像与边序列生动态图 0.2表示每0.2s换一帧四. 效果


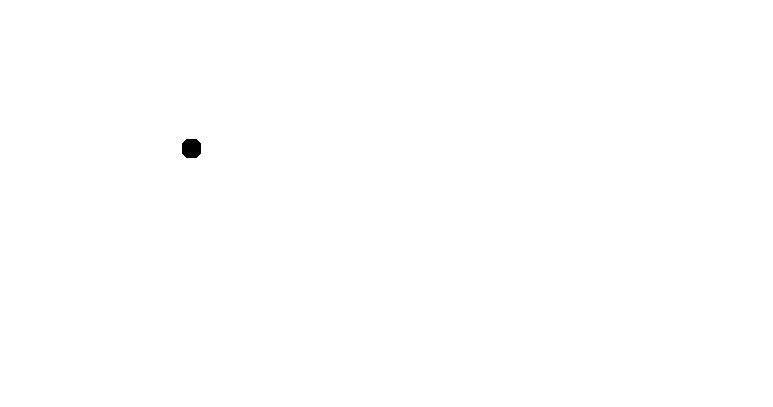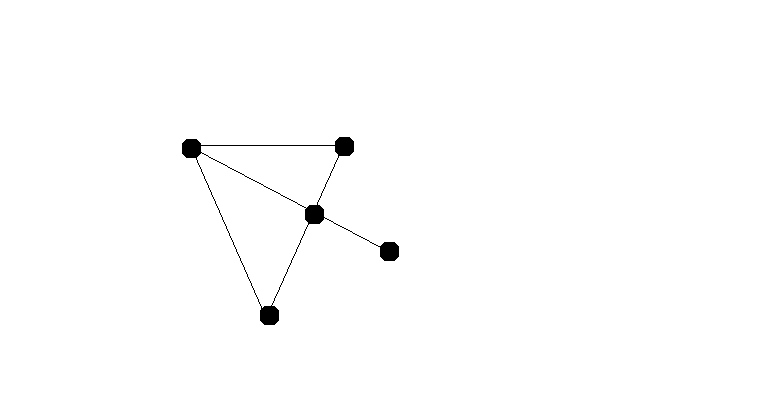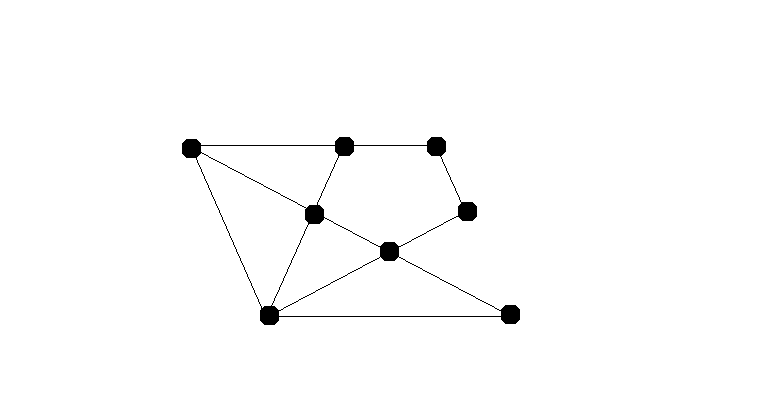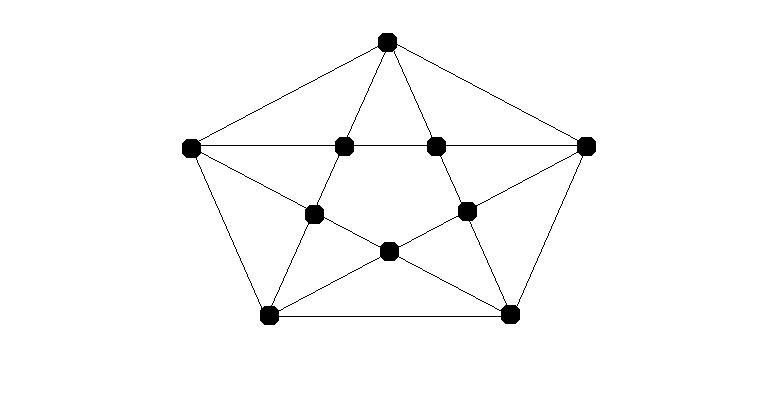

暂无评论