扯淡前言
这个算法是我在研究一个完全不是为了解决它的问题时无意发现的。在写点检测算法的过程中,我发现本该检测出多个点的图像居然出现了一条白线。这引起我的兴趣。复盘一下程序的流程,弄明白为什么会这样后。我发现这个算法适合用来检测一张几何图的所有桥。经过调整与测试后,我给出一个桥检测算法。
一. 目标
输入一张图,检测这样图的所有桥,作为另一张图输出
二. 思路
一张图中的所有桥,区别于其他边的特点是:
- 在桥上任意去除一点都会使原图不连通
据此,将原图细化为但像素脉络图。逐个去除边上的每个像素点及其周围的 3x3 领域,分析去除前后原图的连通分支数是否增加。
- 若是,记录该像素点
- 否则,什么都不做。
遍历完成后将记录的像素点在另一张图将记录点一一显示出来,该图即为答案
三. 步骤
step1. 原图二值化,取反(设为 f)
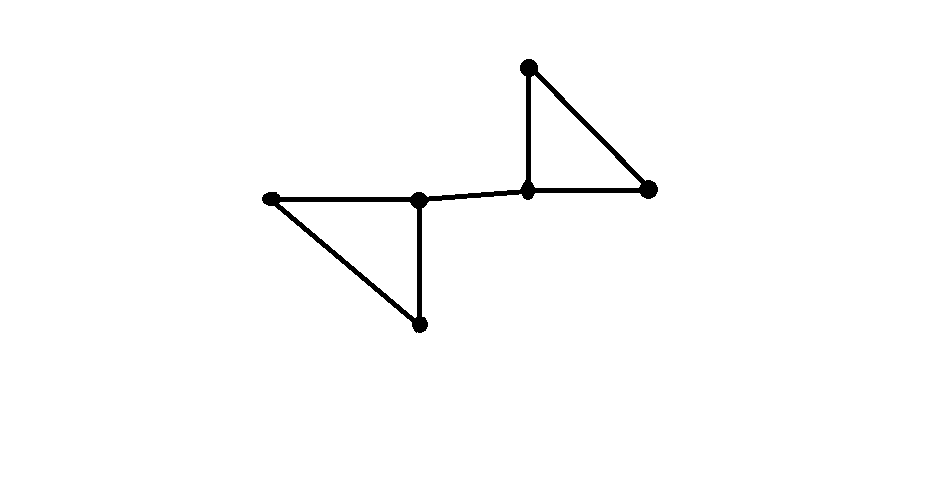
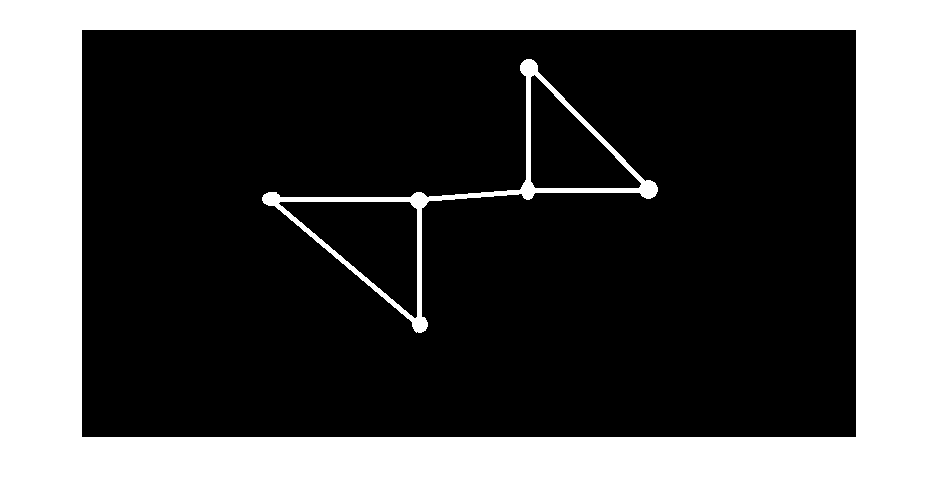
step2. 把图 f 细化为脉络图 g,计数 g 的连通域个数 n1
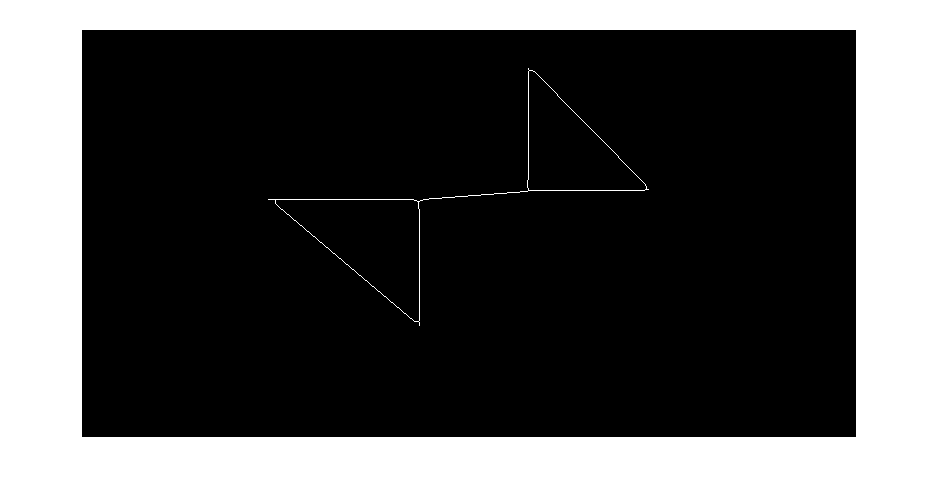
step3. 分析图 g 的每个点及其 8 邻域去除前后对连通域的影响,记录下有影响的点
- 初始化 map 图为全 0 矩阵。
遍历 g 的每个像素点。
若当前像素点为 1 (是图的边),拷贝 g 为 g2,在 g2 将当前遍历的像素点及其 8 邻域的点置 0,计数 g2 连通域个数 n2。
- 若 n2 ≠ n1 (说明访问的点是桥上的点),在 map 上将同一像素点置 1
遍历前的 map

遍历后的 map

step4. map 图去噪,取反,即为原图对应的桥
设一个阈值,将 map 种所有连通域面积小于该阈值的连通块删除。
解释一下,这里之所以会有点状噪声,是因为原图交点处有分叉。

取反

四. 实现
代码
%% 找到一张图所有的桥
%% 输入:一张几何图f
%% 输出:该图的桥h,同时弹出原图二值图与该图的桥对比图
function h=find_bridge(f)
f=im2bw(f);
subplot(121),imshow(f),title '原二值图';
f=~f;
origin=f;
f=bwmorph(f,'thin',inf);
map=zeros(size(f));
[~,num]=bwlabel(f);
for i=2:size(f,1)-1
for j=2:size(f,2)-1
if f(i,j)==0
continue;
end
g=f;
g(i-1,j-1)=0;
g(i-1,j)=0;
g(i-1,j+1)=0;
g(i,j-1)=0;
g(i,j)=0;
g(i,j+1)=0;
g(i+1,j-1)=0;
g(i+1,j)=0;
g(i+1,j+1)=0;
[~,num2]=bwlabel(g);
if num~=num2
map(i,j)=1;
end
end
end
[bridge,n]=bwlabel(map);
stats=regionprops(bridge);
for i=1:n
if stats(i).Area<20
bridge(bridge==i)=0;
end
end
se=strel('disk',4);
bridge=imdilate(bridge,se);
h=double(origin).*bridge;
h=~h;
subplot(122),imshow(h),title '找到的桥';
end测试用例
输入命令

执行效果
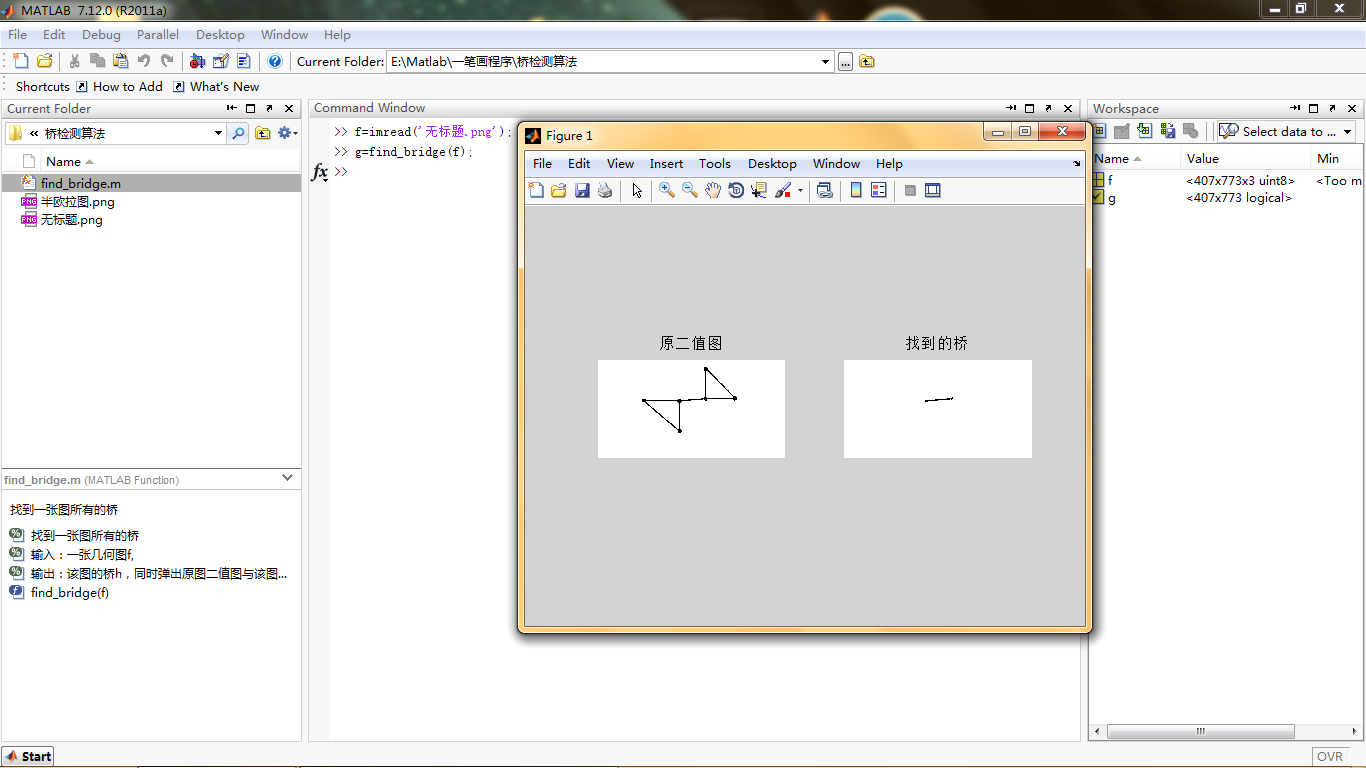
暂无评论