前言

这篇文章是我三年前写的。当时刚接触 matlab，在一次做实验时突然发现执行如下语句

imshow(floor(rand(25)*2)); % 打印一个0-1随机矩阵对应的图像

就会出现一个跟二维码长得很像的图片。

这个发现让我花了一个晚上去想二维码到底是怎么生成的，然后设计了一套(属于自己的)二维码编码/解码 api。

原理

1. 将一个网址(字符串) 映射为一个 n 位二进制串
2. 二进制串转化为一个 0-1矩阵
3. 0-1矩阵生成一张二维码图像 （利用上面的 imshow() api）

步骤

1. 字符串映射为二进制串

{ 所有字母的集合} U { 所有标点的集合 }，字符 总数为 (26 * 2 + 41) = 93 个，每个字符按序分别赋权 1-93，然后用哈夫曼编码，就可以将每一个字符映射到唯一的二进制数。

把网址的每个字符一一替换为二进制数后拼接在一起，就形成二进制串

注：以前这里自己没说清楚。二进制编码算法那么多，为什么用哈夫曼算法？为什么所有字符替换二进制数后可以直接拼接？

这是因为哈夫曼编码的二进制串，在解码时不会有有歧义，任何一个字符的编码，都不会成为其他字符的前缀。

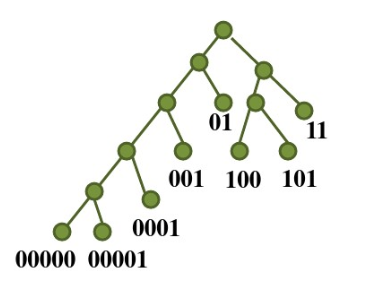
如图，对任意一棵树，如果只在它的叶子节点定义二进制串，那么任何节点上面的编码，都不会成为其他节点的前缀。

这样的话，每个字符编码后拼接后，可以保证对二进制串的解读是唯一的。这就是使用哈夫曼的理由。

1. 将二进制串转化为二进制矩阵

定义一个 25 * 25 的全 0 矩阵，按行覆盖写入二进制串，并预留后十位填入二进制串长度

1. 二进制矩阵用 matlab 读入并保存，得到二值图像一张（就是 “二维码”）

实现

将一个网址编码为二维码图像

%% 将给定字符串转化为二值图像
%% 函数的使用 erweima(str, pth)
%% 输入:
%%   str： 一个合法的网址
%%   pth:  图像保存路径(含文件名)
%% 输出:
%%   无

function code=erweima(str, pth)
    symbols='ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz`1234567890-=[]\;,./~!@#$%^&*()_+{}|:"<>?';
    counts=1:93;
    seq=[];
    for i=1:length(str)
        for j=1:93
            if str(i)==symbols(j)
                seq=[seq j];
            end
        end
    end

    code=arithenco(seq,counts);
    for i=10:30
        if length(code)+20<i*i
            rank=i;
            break;
        end
    end

    truelength=dec2bin(length(code));
    j=1;
    for i=rank*rank+1-length(truelength):(rank*rank)
        code(i)=truelength(j)-48;
        j=j+1;
    end

    lstr=dec2bin(length(str));
    j=1;
    for i=rank*rank-9-length(lstr):(rank*rank)-10
        code(i)=lstr(j)-48;
        j=j+1;
    end

    for i=bin2dec(truelength)+1:rank*rank-20
        code(i)=1;
    end

    code=reshape(code,rank,rank)
    imshow(code);
    imwrite(code,pth,'bitdepth',1);
end

将一张二维码图像解码为网址

%% 将给定二值图像转化为字符串
%% 函数的使用  str=wangzhi(pth)
%% 输入
%%   pth: 图像路径
%% 输出
%%   str: 解码字符串

function str=wangzhi(pth)
    symbols='ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz`1234567890-=[]\;,./~!@#$%^&*()_+{}|:"<>?';
    code=imread(pth);
    code=double(reshape(code,1,length(code)*length(code)));
    
    counts=1:93;
    lseq=[];
    for i=length(code)-19:length(code)-10
        lseq=[lseq code(i)];
    end
    
    lseq=bin2dec(num2str(lseq));
    truelength=[];
    for i=length(code)-9:length(code)
        truelength=[truelength code(i)];
    end
    
    truelength=num2str(truelength);
    code=code(1:bin2dec(truelength));
    dseq = arithdeco(code,counts,lseq);
    str=symbols(dseq);
end

实际操作过程中发现 matlab 自带的 huffman api 编码老出错，阅读手册后改成了官方推荐的 arithenco api，直接解决。

效果

编码(将网址加密成二维码)

解码(从二维码图解密网址)

分析改进

• 缺点

虽然实验证明 api 是可行的。但是，这个算法有一个明显的缺点，就是对图像的精确度要求过高。

因为哈夫曼编码无法容许任何一位数据的丢失或误写。试想编码出来的二维码如果打印上去是模糊的话，那读取方的麻烦就大了。

如果只是读写电脑或手机里存放的图像的话，那没问题。但要在复杂环境下拍照识别估计会很坑。

• 改进

改进的关键在提高二维码容错率。

即使是一个含80个字符的网址，存储成0-1矩阵也只要25*25也绰绰有余。既然存储空间实际上很节省，那么可以把一副二维码进行四等分如下：

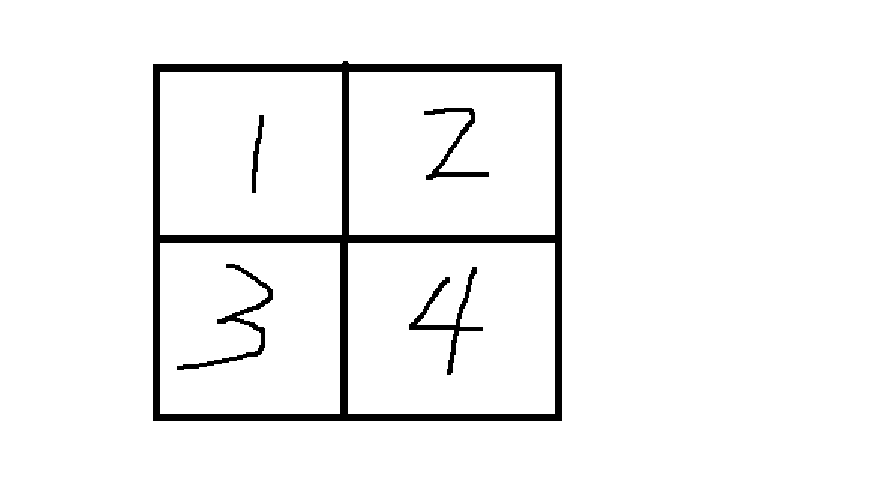
1、2、3、4区域分别用四种编码方案进行图像生成。在解码图像的时候，分别从四个区域入手得到四种答案。如果四种答案一致，那么这个字符串就没有错，否则就将同一位置上出现的字符就四种答案中的出现次数进行比较，选频率高者为最终答案。

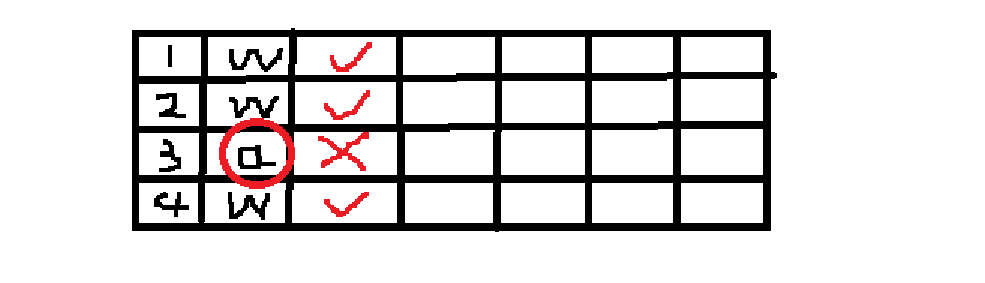
这样做的作用是减少因图像部分显示不全或本身模糊造成的误读，提高容错率。