前言
两年前在网上见过这么一个问题

当时第一眼这不就是一个运筹学的问题么,而且我也刚学 lingo,于是顺手在图书馆花了一个上午把这道题解决了。现在在知乎又看到,想起来翻了翻过去的帖子,发现被删了。。。
没办法,凭借当年留下的程序和一点记忆,我决定把这个问题研究一下。给出更完整的答案。
简单的情况

12 条规则中 6 和 7 带有一定的主观性,不易控制。
不妨假设 6 和 7 得失的点数相抵,先只考虑剩下的确定因素,可以列方程:

- x ≠ 1,是因为 2,3 这两个数字可以组合出除了1之外的任意自然数(包括都不选),排除6 7后一个角色一天能获得的点数也是如此
- 7 - 2j + ∑,代表每人每天所持有点数
用 lingo 求解该方程组
sets:
GIRL/1..5/;
DATE/1..15/;
GD(GIRL,DATE):x;
DD(DATE,DATE)|&1#GE#&2;
endsets
@for(GD(i,j):@gin(x(i,j))); !限制 x 为正整数;
@for(GD(i,j):@abs(x(i,j)-1)>.01); ! x 不等于 1;
@for(GD(i,j):7-2*j+@sum(DD(j,k):x(i,k))>1); !每天每人所持点数必须大于 0;
@for(GD(i,j):7-2*j+@sum(DD(j,k):x(i,k))<10); !每天每人所持点数不超过 10;
@for(DATE(j):@sum(GIRL(i):x(i,j))<7); !男生每天可以分发的点数上限为 7;。。。
它告诉我们没有可行解
这意味着不考虑吃饭,不考虑 7p 以外的点数, 5 个人全员存活是不可能的。
退而求其次,把人数减少为 4,倒是 ok

这说明全员获救为目标的话,我们需要第 7 条规则来增加额外的点数
完整的讨论
现在把 6 7 考虑进去,看看模型会发生什么变化
- 每一餐消费 1P,在能维持生存的前提下越少越好
首先就餐安排是十分主观的因素。在这么拮据的情况下一日多餐肯定不太现实(可以算一下,1日2餐的话,男主每天就需要额外贡献 10P。。而且根据上面还不能保证全员存活)
一般的话一天一餐应该比较稳妥,两天一餐甚至三天一餐也不是没有可能。不太好说,可以把它作为一个调节参数,通过修改它调整策略。
- 意思是超过 7P 后每一次点数的收益从 2, 3P 降为 1P
理论上讲男主可以利用这条规则不断产生点数来保证全员存活,但为保护男主次数也是越少越好。因此适合作为优化目标。
现将 6 7 加入约束条件
- 引入一个就餐表
meal(i,j):表示第 i 个女生第 j 天是否吃饭。(非 0 即 1, 0 表示不吃,1表示吃饭)
- 定义就餐周期,用餐次数
X_DAYS_Y_MEAL
Y_MEAL_X_DAYS
重新定义一些基本变量
- get(i,j):表示第 i 个女生第 j 天获得点数
- status(i,j):表示第 i 个女生第 j 天所持点数
- h(j):表示第 j 天一共给了多少次
- minimum_h_times: 平均每日次数 (优化目标)
整合后代码如下:
data:
H_TIMES = 8; !每天次数上限;
X_DAYS_Y_MEAL = 3; !几日一餐;
Y_MEAL_X_DAYS = 2; !用餐次数;
enddata
sets:
GIRL/1..5/;
DATE/1..15/:h;
GD(GIRL,DATE):get,meal,status; !get代表每人每天获得P数,meal代表是否就餐,status代表每人每天所持P数;
DD(DATE,DATE)|&1#GE#&2;
GD1(GIRL,DATE);
GD2(GIRL,DATE,DATE)|(&2+1#EQ#&3);
GD3(GIRL,DATE,DATE,DATE)|(&2+1#EQ#&3)#AND#(&2+2#EQ#&4);
GD5(GIRL,DATE,DATE,DATE,DATE,DATE)|(&2+1#EQ#&3)#AND#(&2+2#EQ#&4)#AND#(&2+3#EQ#&5)#AND#(&2+4#EQ#&6);
endsets
data:
@OLE('E:\lingo\solution.xlsx', 'get', 'meal')=get, meal; !将结果输出到 excel 文件;
enddata
@for(GD(i,j):@gin(get(i,j))); !限制 get 为自然数;
@for(DATE(j):@sum(GIRL(i):get(i,j)) < H_TIMES + 4);
@for(GD(i,j):status(i,j) = 7 - 2*j + @sum(DD(j,k):get(i,k)-meal(i,k))); !计算每人每天所持点数;
@for(GD(i,j):status(i,j)>.01); !每人每天所持点数必须大于 0;
@for(GD(i,j):status(i,j)<10); !每人每天所持点数不能超过 10;
@for(DATE(j):h(j) = @sum(GIRL(i):get(i,j))-7+3); !计算每天给予点数的次数;
@for(DATE(j):@abs(h(j)-MINIMUM_H_TIMES)<1); !每天次数应尽量均匀分布;
@for(GD(i,j):@bin(meal(i,j))); !限制 meal 为 0-1 变量;
!@for(GD1(i,j):meal(i,j)>Y_MEAL_X_DAYS); !保证每人每周期的用餐次数,下同;
!@for(GD2(i,j,k):meal(i,j)+meal(i,k)>Y_MEAL_X_DAYS);
@for(GD3(i,j,k,l):meal(i,j)+meal(i,k)+meal(i,l)>Y_MEAL_X_DAYS);
!@for(GD5(i,j,k,l,o,q):meal(i,j)+meal(i,k)+meal(i,l)+meal(i,o)+meal(i,q)>Y_MEAL_X_DAYS);
minimum_h_times = @sum(DATE(j):h(j)) / 15;
MIN = minimum_h_times;不断调整次数上限,用餐安排三个参数,就能解出最优决策。
我试了一下,大致规律如下:
| X_DAYS_Y_MEAL | MINIMUM_H_TIMES |
|---|---|
| 1 日 1 餐 | 9 |
| 3 日 2 餐 | 8 |
| 5 日 3 餐 | 7 |
| 5 日 2 餐 | 6 |
| 4 日 1 餐 | 5 |
对 5 名女生,最稳妥的方案当然是 1 日 1 餐,但 1 日 9 次且不论现实与否,对男主确实不太友好。
个人比较倾向于 5 日 3 餐这个方案。
为什么呢?因为 3 日 2 餐意味着 1.5 天一顿,而 5 日 3 餐是 1.6 天 一顿。差别不大但是却能让男主平均每天少给1 次。5 日 2 餐虽然次数减少了 1,但是但代价却是每人 2.5 天一顿,用餐周期几乎延长了 1 天。
当然了,具体选哪个,这也是见仁见智。
附:各种方案下的生存策略
1 日 1 餐
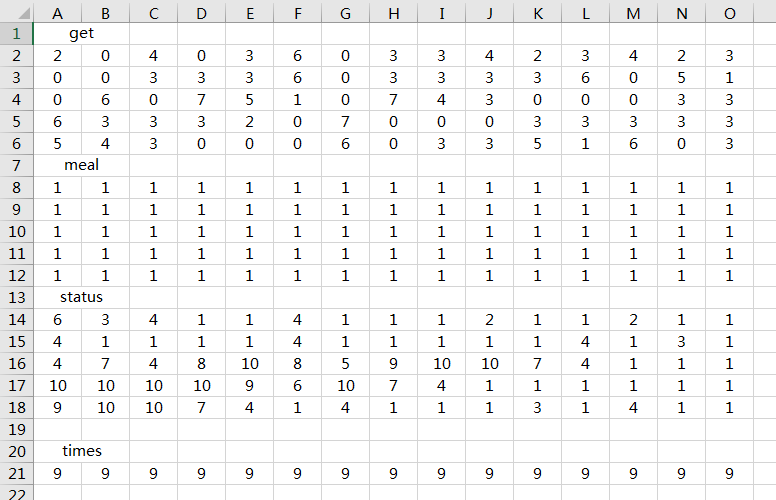
2 日 1 餐
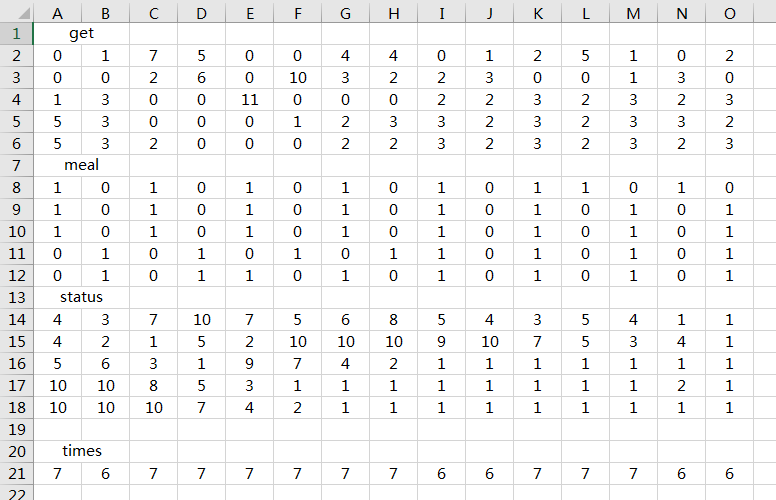
3 日 1 餐
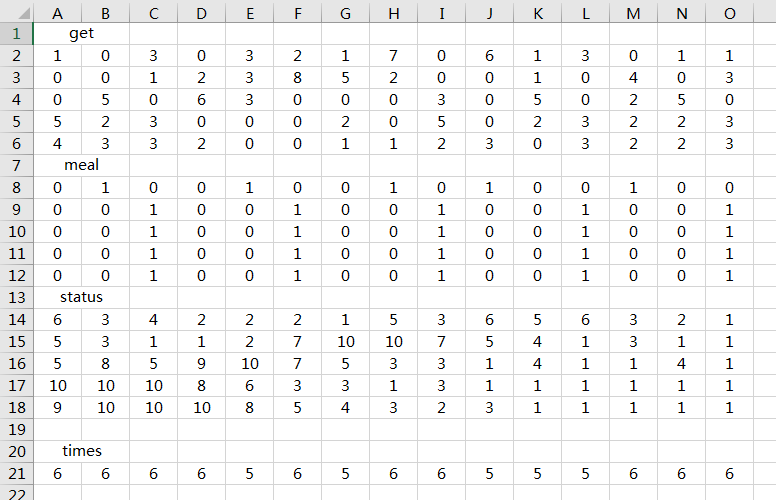
3 日 2 餐
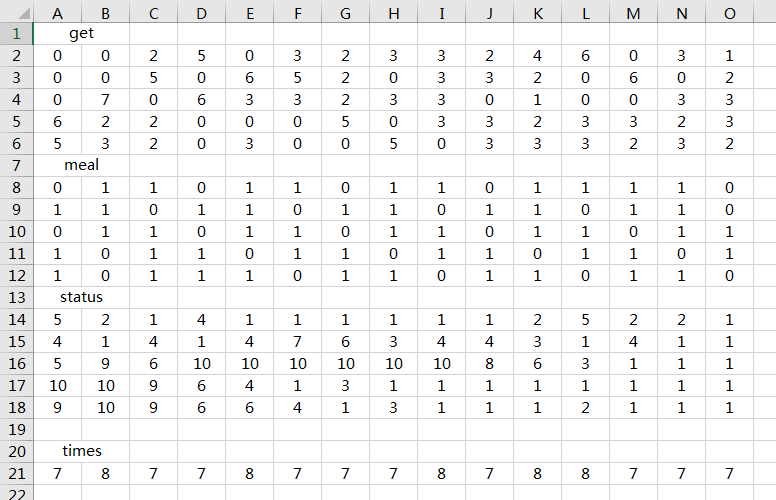
5 日 3 餐
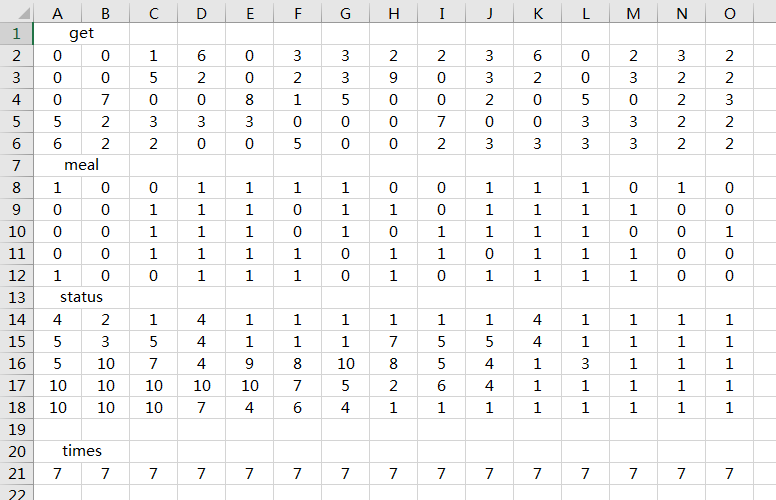
5 日 2 餐
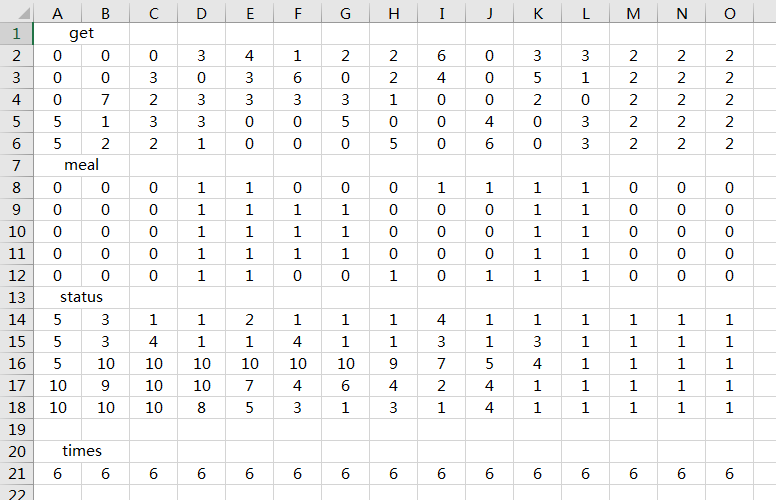
一点改进
突然想到,如果因为某些原因,游戏进行中被剧情打乱计划怎么办,15天前的决策分分钟就可能不再是最优解。
所以更稳定的做法是:在计划赶不上变化时,根据每一天结束时的状态进行动态决策。
这也不难,只要抽离幸存人数,剩余天数,每人初始 P 点这几个常数作为调节参数就行。
data:
H_TIMES = 8; !每天次数上限;
X_DAYS_Y_MEAL = 3; !几日一餐;
Y_MEAL_X_DAYS = 2; !用餐次数;
GIRLS_NUM = 5; !幸存者数;
SURVIVE_DAYS = 15; !剩余天数;
enddata
sets:
GIRL/1..GIRLS_NUM/:P;
DATE/1..SURVIVE_DAYS/:h;
GD(GIRL,DATE):get,meal,status; !get代表每人每天获得P数,meal代表是否就餐,status代表每人每天所持P数;
DD(DATE,DATE)|&1#GE#&2;
GD1(GIRL,DATE);
GD2(GIRL,DATE,DATE)|(&2+1#EQ#&3);
GD3(GIRL,DATE,DATE,DATE)|(&2+1#EQ#&3)#AND#(&2+2#EQ#&4);
GD5(GIRL,DATE,DATE,DATE,DATE,DATE)|(&2+1#EQ#&3)#AND#(&2+2#EQ#&4)#AND#(&2+3#EQ#&5)#AND#(&2+4#EQ#&6);
endsets
data:
@OLE('E:\lingo\solution.xlsx', 'get', 'meal')=get, meal; !将结果输出到 excel 文件;
enddata
data:
p = 7 7 7 7 7; !输入每人初始P数;
enddata
@for(GD(i,j):@gin(get(i,j))); !限制 get 为自然数;
@for(DATE(j):@sum(GIRL(i):get(i,j)) < H_TIMES + 4);
@for(GD(i,j):status(i,j) = p(i) - 2*j + @sum(DD(j,k):get(i,k)-meal(i,k))); !计算每人每天所持点数;
@for(GD(i,j):status(i,j)>.01); !每人每天所持点数必须大于 0;
@for(GD(i,j):status(i,j)<10); !每人每天所持点数不能超过 10;
@for(DATE(j):h(j) = @sum(GIRL(i):get(i,j))-7+3); !计算每天给予点数的次数;
@for(DATE(j):@abs(h(j)-MINIMUM_H_TIMES)<1); !每天次数应尽量均匀分布;
@for(GD(i,j):@bin(meal(i,j))); !限制 meal 为 0-1 变量;
!@for(GD1(i,j):meal(i,j)>Y_MEAL_X_DAYS); !保证每人每周期的用餐次数,根据实际周期三选一;
!@for(GD2(i,j,k):meal(i,j)+meal(i,k)>Y_MEAL_X_DAYS);
@for(GD3(i,j,k,l):meal(i,j)+meal(i,k)+meal(i,l)>Y_MEAL_X_DAYS);
!@for(GD5(i,j,k,l,o,q):meal(i,j)+meal(i,k)+meal(i,l)+meal(i,o)+meal(i,q)>Y_MEAL_X_DAYS);
MINIMUM_H_TIMES = @sum(DATE(j):h(j)) / SURVIVE_DAYS;
MIN = MINIMUM_H_TIMES;理论上讲,只要保证两点:
- 严格执行最优方案
- 男主自己跟得上
毫无疑问 galgame《神様のゲーム -監禁された6人の男女》中是可以全员存活的。
暂无评论