曲线拟合

接上篇文章。用多项式拟合，有两种方式。一种是构造法方程组，解法方程组。另一种是生成自变量，问题看成多元线性回归，矩阵求广义逆。

这里用第二种方法，先用 excel 尝试

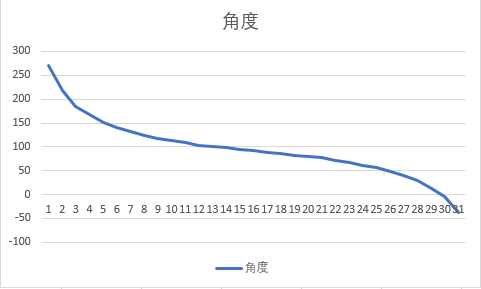
拟合前

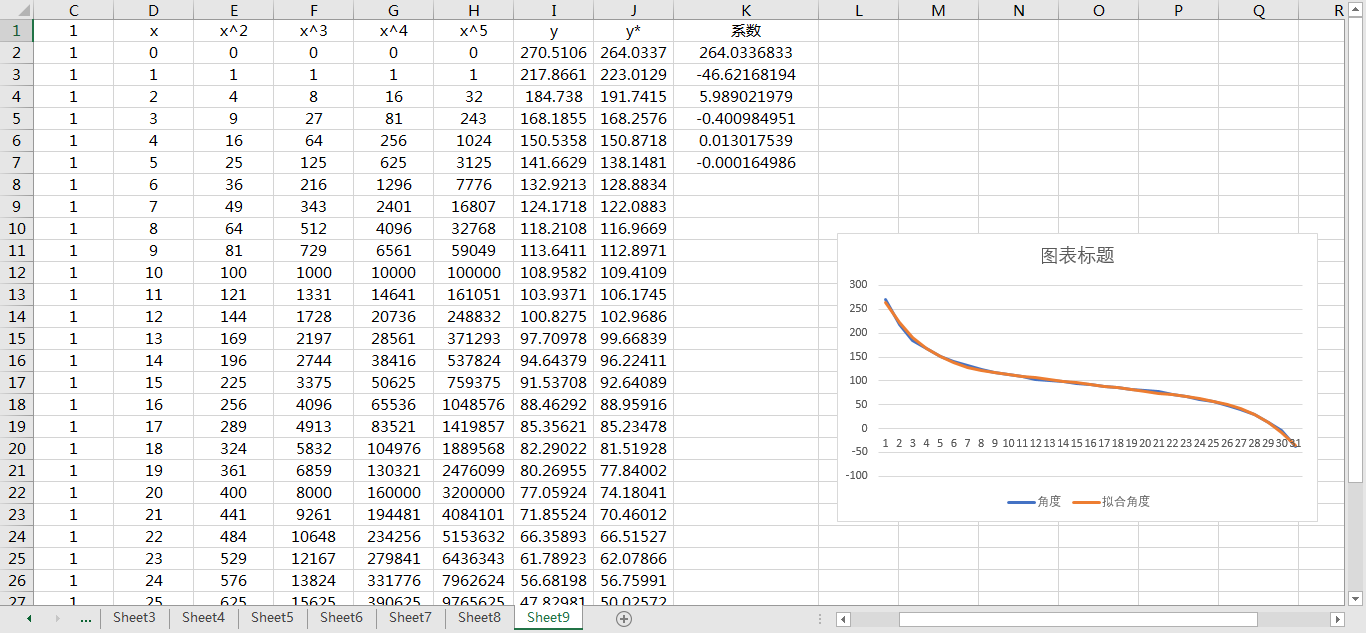
拟合后

将之前代码的系数改一下

// 这里
[254.5074303, -41.48808654, 5.18375032, -0.348365691, 0.011489067, -0.000148665]
// 改成
[264.0336833, -46.62168194, 5.989021979, -0.400984951, 0.013017539, -0.000164986]

效果如下

代码

一开始因为解方程需要矩阵求逆的原因，是不想写代码的。直到网上找到了 math.js 这个库，突然发现 js 可以算矩阵了。真爽，一下就把难题解决了

多项式拟合 api

 /*
  * @description：多项式拟合
  * @params {Object} points: 待拟合点，格式为 [{x, y}, ...]
  * @params {Number} pow: 多项式次数
  * @return {Object}：多项式系数，拟合误差，格式为 {coef, error}
  */
function polyFit(points, pow) {
  let eqns = mkEquations(points, pow),
  coef = solveEquations(eqns),
  error = evaluateFit({coef, points})
  return {coef, error}
}

// 列方程组
function mkEquations(points, pow) {
  let A = points.map(p => {
    let row = []
    for(let i=0; i<=pow; i++) row.push(p.x ** i)
    return row
  })
  let b = points.map(p => p.y)
  return {A, b}
}

// 解方程组
function solveEquations({ A, b }) {
  let APlus = math.multiply(math.inv(math.multiply(math.transpose(A), A)), math.transpose(A))
  return math.multiply(APlus, b)
}

// 计算拟合误差
function evaluateFit({ coef, points }) {
  let x = points.map(p => p.x)
  y1 = points.map(p => p.y),
  y2 = x.map(x => solvePoly(coef, x)),
  error = y2.reduce((ans, y, i) => ans + Math.abs(y2[i] - y1[i]), 0) / y2.length
  return error
}

// 代多项式
function solvePoly(coef, x) {
  return coef.reduce((ans, c, pow) => ans + c * (x ** pow), 0)
}

这样用：

let points = [
        {x: 0, y: 270.5106441},
        {x: 1, y: 217.8660688},
        {x: 2, y: 184.7380098},
        {x: 3, y: 168.1855387},
        {x: 4, y: 150.5357905},
        {x: 5, y: 141.6628906},
        {x: 6, y: 132.9213410},
        {x: 7, y: 124.1717714},
        {x: 8, y: 118.2107661},
        {x: 9, y: 113.6410719},
        {x: 10, y: 108.9581834},
        {x: 11, y: 103.9370730},
        {x: 12, y: 100.8274531},
        {x: 13, y: 97.70977658},
        {x: 14, y: 94.64379413},
        {x: 15, y: 91.53708498},
        {x: 16, y: 88.46291502},
        {x: 17, y: 85.35620587},
        {x: 18, y: 82.29022342},
        {x: 19, y: 80.26955092},
        {x: 20, y: 77.05923984},
        {x: 21, y: 71.85523554},
        {x: 22, y: 66.35892806},
        {x: 23, y: 61.78923391},
        {x: 24, y: 56.68197776},
        {x: 25, y: 47.82980759},
        {x: 26, y: 39.13845860},
        {x: 27, y: 29.46420949},
        {x: 28, y: 12.81789710},
        {x: 29, y: -4.73800982},
        {x: 30, y: -37.05485468}
]

let poly = polyFit(points, 5)

// {coef: [264.0336832917178, 
//        -46.621681946883854, 
//         5.989021977896223, 
//        -0.4009849509054618, 
//         0.013017538778813481,
//        -0.0001649859462062585], 
//  error: 1.8659154769107695}

1.8 度的误差， 也就是 360 度的 1 / 200，轨迹的精度在 99.5% 左右