每次打开电脑总会有这个 loading 动画,看上去挺优雅的,就想着怎么把它弄到自己的项目上。
写一个 loading 动画对前端来说不难,但是要精确模拟小球的运动轨迹就有难度了。想法一直都有,但是往往在数据收集这一步就因为麻烦劝退了。
最近上网看到 loading 动画的 gif 图,刚好对这个项目有帮助,就一鼓作气把它折腾出来。

执行计划
- 第一步,数据的采集,以时间为单位采集小球的坐标,角度数据。(t, x), (t, y), (t, θ) 这样
- 第二步,逆向离散的数据点,重构描述运动规律的函数
- 第三步,写代码,将 loading 动画在前端重现
数据的采集
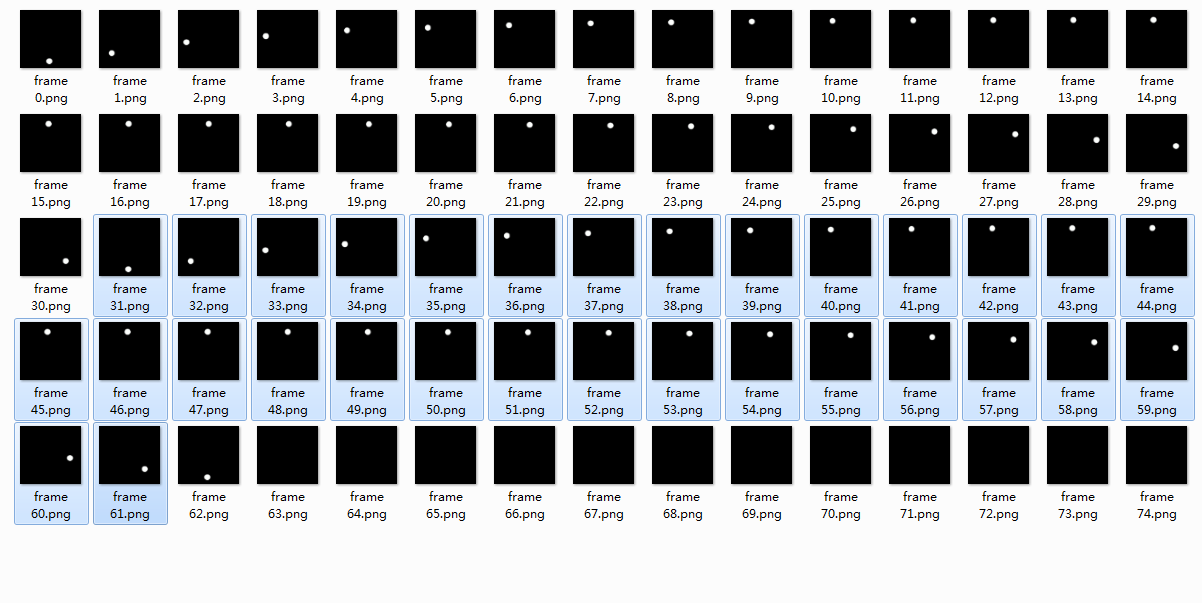
分解 loading 动图,抽离出每一帧画面

假设 5 个小球的行为是一样的,那么只分析 1 个小球,搞清它的运动模式后,拷贝 4 个模式相同的小球就可以。这里就用 windows 的画图工具处理掉其它小球,保留第一个
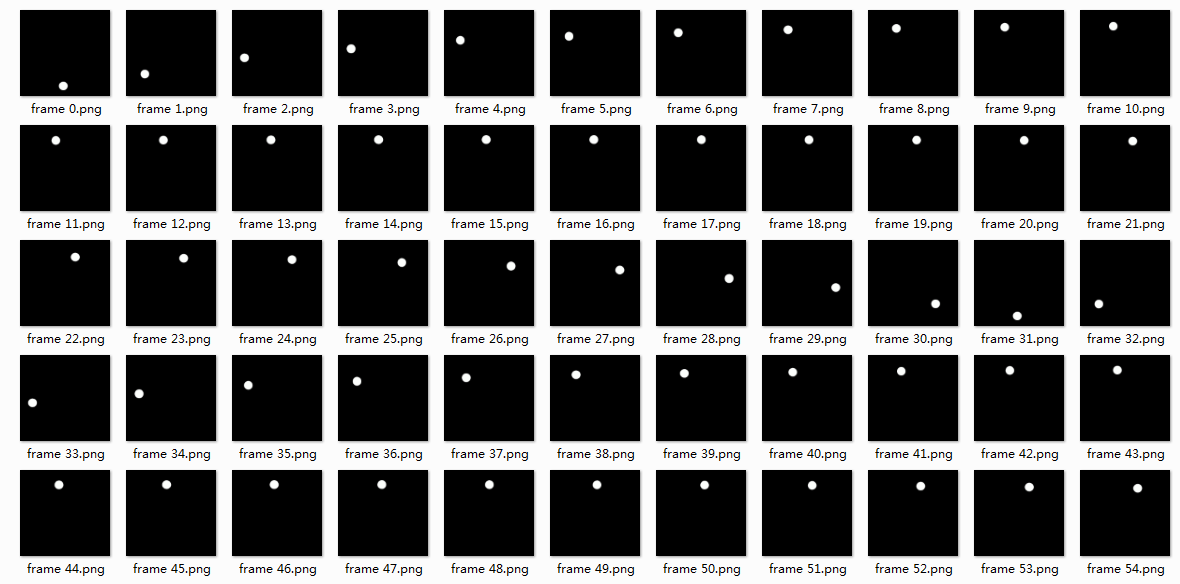
从单个来看的话,小球运动动画是这样的

从分解的静图看,一共 75 帧。小球从正下方出现,转 2 圈回到起点后消失,等待 12 帧后重新出现,开始循环。
由于只有两种颜色,所以这里采用图像识别方法处理所有截图,获取数据。虽然 js 没有专门的图像处理模块,但好在浏览器有 canvas。利用这点就够了。
从图像到数据,大概原理就是过滤像素,筛选出小球的所有像素点,然后再根据小球左右上下对称的特点,利用以下方式算小球坐标
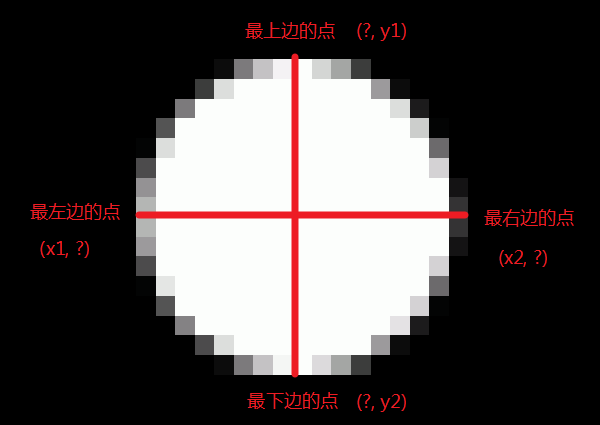
以 ((x1 + x2)/2, (y1 + y2)/2) 为圆心坐标,代替小球位置。
代码见后边,过程戳这里。总之,一顿操作后可以拿到小球的运动数据
| 时间 | x | y |
|---|---|---|
| 0 | 80 | 17.5 |
| 1 | 35 | 39 |
| 2 | 24 | 69 |
| 3 | 25 | 85 |
| 4 | 31 | 101 |
| 5 | 36 | 108 |
| 6 | 41 | 115 |
| 7 | 48 | 120 |
| 8 | 53 | 123 |
| 9 | 57 | 125 |
| 10 | 61.5 | 126 |
| 11 | 66 | 128 |
| 12 | 69 | 128.5 |
| 13 | 72 | 129 |
| 14 | 75 | 129 |
| 15 | 78 | 129.5 |
| 16 | 81 | 129.5 |
| 17 | 84 | 129 |
| 18 | 87 | 129 |
| 19 | 89 | 129 |
| 20 | 92 | 128 |
| 21 | 97 | 127 |
| 22 | 102 | 125 |
| 23 | 106 | 123 |
| 24 | 110 | 120 |
| 25 | 117 | 115 |
| 26 | 123 | 109 |
| 27 | 128 | 101 |
| 28 | 134 | 86 |
| 29 | 135 | 69 |
| 30 | 124 | 40 |
| 31 | 80 | 17.5 |
| 32 | 35 | 39 |
| 33 | 24 | 69 |
| 34 | 25 | 85 |
| 35 | 31 | 101 |
| 36 | 36 | 108 |
| 37 | 41 | 115 |
| 38 | 48 | 120 |
| 39 | 53 | 123 |
| 40 | 57 | 125 |
| 41 | 61.5 | 126 |
| 42 | 66 | 128 |
| 43 | 69 | 128.5 |
| 44 | 72 | 129 |
| 45 | 75 | 129 |
| 46 | 78 | 129.5 |
| 47 | 81 | 129.5 |
| 48 | 84 | 129 |
| 49 | 87 | 129 |
| 50 | 89 | 129 |
| 51 | 92 | 128 |
| 52 | 97 | 127 |
| 53 | 102 | 125 |
| 54 | 106 | 123 |
| 55 | 110 | 120 |
| 56 | 117 | 115 |
| 57 | 123 | 109 |
| 58 | 128 | 101 |
| 59 | 134 | 86 |
| 60 | 135 | 69 |
| 61 | 124 | 40 |
| 62 | 80 | 17.5 |
| 63 | NaN | NaN |
| 64 | NaN | NaN |
| 65 | NaN | NaN |
| 66 | NaN | NaN |
| 67 | NaN | NaN |
| 68 | NaN | NaN |
| 69 | NaN | NaN |
| 70 | NaN | NaN |
| 71 | NaN | NaN |
| 72 | NaN | NaN |
| 73 | NaN | NaN |
| 74 | NaN | NaN |
从数据逆向轨迹函数
周期里的周期
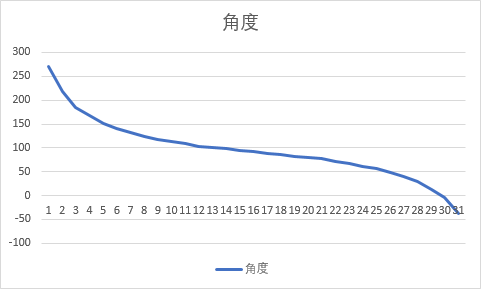
忽略小球消失的 12 帧,画出时间-横坐标图
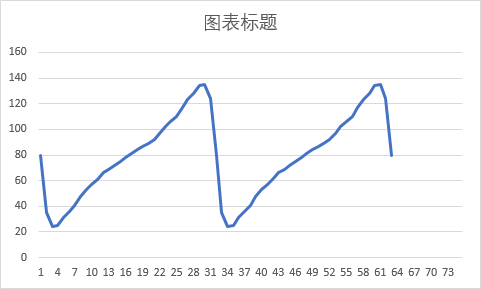
注意到这个图呈现的周期性,首先它有两个相同的山峰,其次首尾数据都是 80,连在一起刚好是两个完整周期。回到数据与帧图。可以发现一个周期对应小球的一次圆周运动。
动图 75 帧,间距 100ms,对应 loading 动画每 7.5s 重复以下的循环一次
- 第 1 到 31 帧(frame0 - frame30),完成一次圆周运动的闭环
- 第 32 到 62 帧(frame31 - frame61),完成第二次圆周运动的闭环(这里就是重复的周期)
- 第 63 帧(frame62),一张小球出现在底部的帧
- 第 64 到 75 帧(frame63 - frame74),小球消失
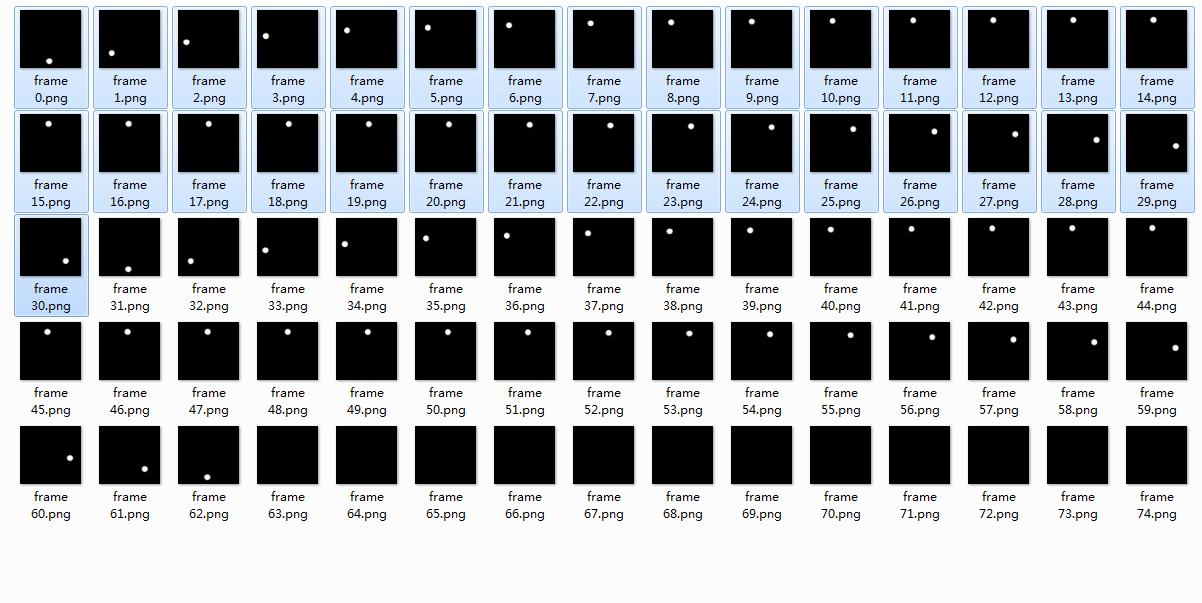


问题可以归结为 1 个周期,第 1 到 31 帧小球的运动轨迹分析
角度的计算
这里有两种策略,一种是把运动轨迹看成坐标关于时间的函数 x = x(t),y = y(t)。另一种是看成角度关于时间的函数 θ = θ(t)
老实说,这之前我已经反解过 x 的函数,但就在做 y 的过程中意识到了函数的不统一,用角度好像更方便。所以后来就用角度计算了
计算角度,首先需要圆心
圆心的计算:
三点定一圆,选择图上距离较远的三点,连接三点作两条弦,两条弦上中垂线的交点就是圆心。
注意这里不用图像处理的任何东西,用现成的数据,找三个坐标直接算就 ok。
圆心计算结果是 (79.5,73.6),知道圆心,就可以计算角度
角度的计算:
所有坐标 (x, y) 减去圆心,得到相对圆心坐标 (rx, ry)。
用反正切 Math.atan2(ry, rx),得到弧度。弧度乘以 180/Math.PI,得到角度。
总之一顿操作后,1 个周期内 (第 0 到第 30 帧) 的角度数据如下:
| 时间 | 角度 |
|---|---|
| 0 | 270.5106 |
| 1 | 217.8661 |
| 2 | 189.6584 |
| 3 | 168.1855 |
| 4 | 151.9887 |
| 5 | 139.8311 |
| 6 | 130.6807 |
| 7 | 123.6918 |
| 8 | 118.1873 |
| 9 | 113.6411 |
| 10 | 109.66 |
| 11 | 105.9663 |
| 12 | 102.3791 |
| 13 | 98.79756 |
| 14 | 95.18208 |
| 15 | 91.53708 |
| 16 | 87.89293 |
| 17 | 84.28812 |
| 18 | 80.75146 |
| 19 | 77.28419 |
| 20 | 73.84221 |
| 21 | 70.31817 |
| 22 | 66.52368 |
| 23 | 62.17144 |
| 24 | 56.85742 |
| 25 | 50.04299 |
| 26 | 41.03714 |
| 27 | 28.97857 |
| 28 | 12.8179 |
| 29 | -8.70021 |
| 30 | -37.0549 |
画图
用多项式插值求解函数。
这里我选择牛顿插值法。分别用 3 次,4 次,5 次多项式等模拟(步骤和代码见后边),结果在 5 次多项式这里找到一个相似度很高的曲线
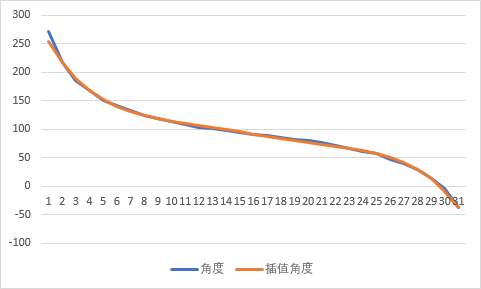

对应表达式:
θ = -0.00015 x^5 + 0.011489 x^4 - 0.34837 x^3 + 5.18375 x^2 - 41.4881 * x + 254.5074
统计两列数据的距离,平均误差 1.694 ,相对于 1 周 360 度,精度已经很高了
如果认为蓝线与红线的不重合处是数据误差的话,那么这个函数可以当作 loading 函数。
一个小球到一堆小球
一帧一帧观察,发现第 2 个球比第 1 个球出现时间慢 3 帧,且同一位置相比第 1 小球逆时针偏移 15 度。
第 3 个小球比第 1 小球慢 6 帧,偏移角度 30 度。第 4 第 5 分别慢 9,12 帧,偏移 45,60 度。
写代码
<style>
.container {
position: relative;
background: #000;
width: 164px;
height: 157px;
}
.ball {
position: absolute;
background: #fcfefc;
border-radius: 50%;
width: 17px;
height: 17px;
opacity: 0;
margin: -8.5px 0 0 -8.5px;
}
</style>
<div class="container">
<div class="ball"></div>
<div class="ball"></div>
<div class="ball"></div>
<div class="ball"></div>
<div class="ball"></div>
</div>class BALL {
constructor(options) {
this.el = options.el
this.offset = options.offset || 0
this.init()
}
init() {
this.t = 0
this.frames = 75
this.cPoint = {x: 79.5, y: 66.6}
this.radius = 55.9
this.loop()
}
loop() {
setInterval(() => {
this.update()
this.render()
}, 100)
}
update() {
let {x, y} = this.getCursor(this.t)
let o = this.getOpacity(this.t)
this.x = x
this.y = y
this.o = o
this.t = (this.t + 1) % this.frames
}
render() {
this.el.style.left = this.x + 'px'
this.el.style.bottom = this.y + 'px'
this.el.style.opacity = this.o
}
getCursor(t) {
let angle = this.getAngle(t)
let rad = angle * Math.PI / 180
let x = this.radius * Math.cos(rad) + this.cPoint.x
let y = this.radius * Math.sin(rad) + this.cPoint.y
return {x, y}
}
getOpacity(t) {
return t > 62 ? 0 : 1
}
getAngle(t) {
t = t % 31
let arr = [254.5074303, -41.48808654, 5.18375032, -0.348365691, 0.011489067, -0.000148665]
let ang = arr.reduce((ret, coef, pow) => ret + coef * (t ** pow), this.offset)
return ang
}
}
// 开始动画
let balls = document.querySelectorAll('.container .ball')
for(let i=0; i<balls.length; i++) {
setTimeout(() => {
new BALL({el: balls[i], offset: 15 * i})
}, 300 * i)
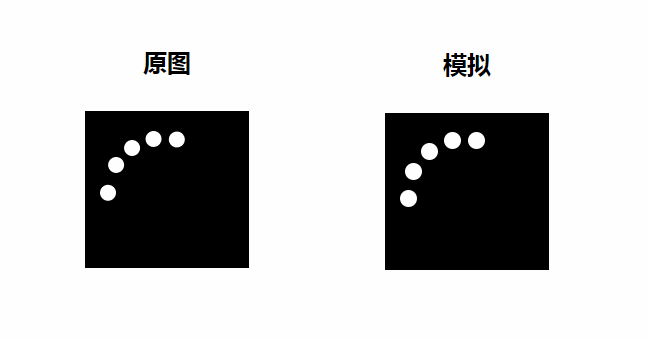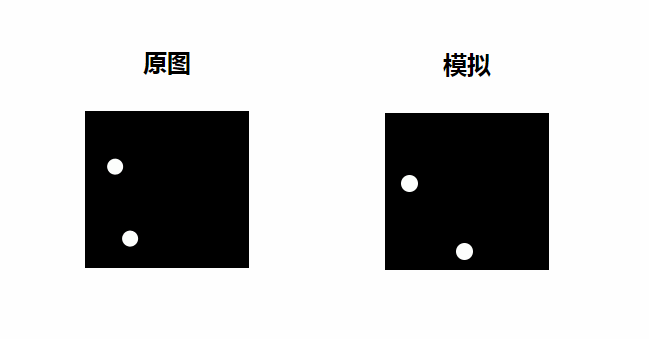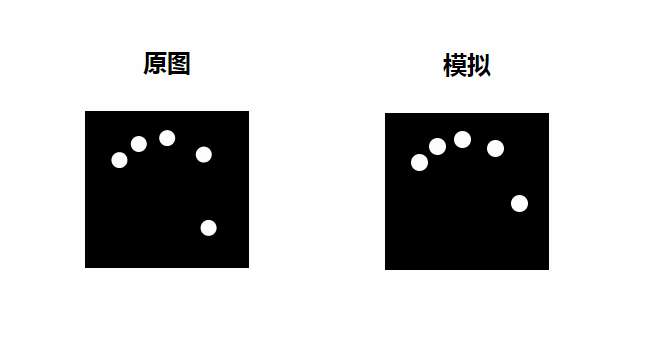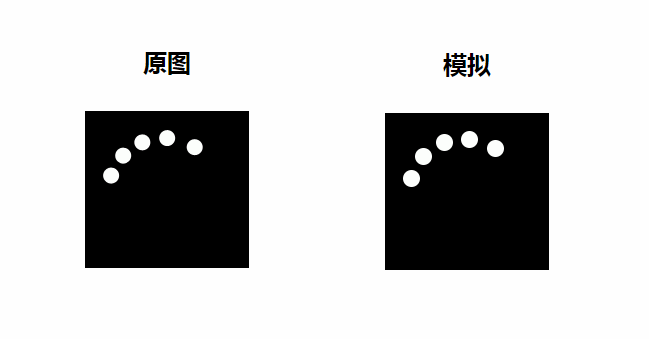
}效果如下

对比原版
杂项
这里总结一下过程中遇到的困难,以及相关代码。
- 角度的计算:知坐标求角度是个难题。感谢 stackoverflow 上的老哥,让我知道 JS 有 atan2 这么好用的 api。托它的福,之前的一篇文章环状滑动选择器的实现与思考,现在有更棒的做法:连接鼠标与圆心,将该向量的坐标换算成角度,用角度更新滑块的位置。
- 获取图片的像素数据:JS 没有直接读取图片像素数据的 api。借助 canvas,封装一个 imread api 解决。
- 插值算法:用牛顿插值法是因为我只记得这个方法,因为差商表算起来很简便。一开始我用 excel 算答案,后来发现插值选点的不同对效果影响很大。所以索性用 JS 封装一个自动插值 api,随机选点,自动优化。
这里比起插值,其实更应该用拟合。因为插值若非完全相等就没有意义。用随机选点那一套本质上还是距离择优,而能将这点做到极致的恰恰是拟合。所以拟合更好,有空再改。
atan2
atan2(y_number, x_number)
返回一个弧度,介于 -PI 到 PI 之间。x 负轴逆时针方向为起点,从 -PI 开始,到 PI 结束
若想获得数学意义上的角度(x 正轴逆时针方向为起点,从 0 开始,到 360 结束),可以
function getDeg(x, y) {
let rad = Math.atan2(y, x)
let deg = rad * 180 / Math.PI
deg = deg < 0 ? deg + 360 : deg
return deg
}获取图片像素数据(imread api)
/*
* @description:输入一张图片,获取该图像素数据并以 "rgbxy" 格式输出
* @params {String} url: 图片地址
* @params {String} cnvSelector: canvas选择器,可空。为空表示不将图片渲染到 canvas 标签,静默获取图片数据
* @return {Object}: rgbxy 对象数组
*/
function imread(url, cnvSelector) {
return new Promise((resolve, reject) => {
try {
let cnv = cnvSelector ? document.querySelector(cnvSelector) : document.createElement('canvas')
let cxt = cnv.getContext('2d')
let img = new Image()
// 没有这句话会产生跨域问题,详见张鑫旭老师的博客
img.crossOrigin = ''
// 图片的地址不能是本地协议,必须是 http 协议
img.src = url
img.onload = function() {
cnv.width = img.width
cnv.height = img.height
cxt.drawImage(img, 0, 0)
let rawImageData = cxt.getImageData(0, 0, cnv.width, cnv.height)
let imageData = parseImageData(rawImageData)
resolve(imageData)
}
} catch(e) {
reject(e)
}
})
}
// 读取原生图像数据,转换成 "rgbxy" 格式
function parseImageData({data, width, height}) {
let rgb = parseRGBData(data)
let rgbxy = parsePositionData(rgb, width, height)
return rgbxy
}
// 解析图像的颜色数据
function parseRGBData(data) {
data = [...data]
let rgb = []
while(data.length > 0) {
let rgba = data.splice(0, 4)
let r = rgba[0]
let g = rgba[1]
let b = rgba[2]
rgb.push({r, g, b})
}
return rgb
}
// 解析图像的位置数据。行列从 1 计数,采用 W3C 坐标系(y 轴正向朝下)
function parsePositionData(rgb, width, height) {
return rgb.map((item, idx) => {
let colIdx = idx % width
let rowIdx = (idx - colIdx) / width
item.x = colIdx + 1
item.y = rowIdx + 1
return item
})
}可以通过以下方式调用。异步是因为图片数据的获取须在图片 onload 触发后执行
imread('http://qn.simenchan.xyz/frame 0.png').then(imageData => console.log(imageData))寻找图像中特定色块的坐标
/*
* @description:寻找图像中特定色块的坐标
* @params {Object} imageData:rgbxy 对象数组
* @params {Object} filter:回调函数,作为像素过滤器,一个参数,代表 rgbxy 数组每个元素
* @return {Object}:过滤器筛选的 像素点集 的坐标中心 {x, y}
*/
function imSearch(imageData, filter) {
let targetRange = imageData.filter(filter)
let width = imageData.slice(-1)[0].x
let height = imageData.slice(-1)[0].y
let xRange = targetRange.map(p => p.x)
let yRange = targetRange.map(p => height - p.y)
console.log(xRange)
console.log(yRange)
let x1 = Math.min.apply(null, xRange)
let x2 = Math.max.apply(null, xRange)
let y1 = Math.min.apply(null, yRange)
let y2 = Math.max.apply(null, yRange)
let x = (x1 + x2) / 2
let y = (y1 + y2) / 2
return { x, y }
}用法
// 假设要找以下色块的位置
const TARGET_COLOR = {r: 252, g: 254, b: 252}
// 先定义过滤器
function pixelFilter(pixel) {
let {r, g, b} = TARGET_COLOR
return pixel.r===r && pixel.g===g && pixel.b===b
}
// 然后调用
let {x, y} = imSearch(imageData, pixelFilter)插值算法(interp api)
手工算法:
这里用到的是牛顿插值法,该方法求多项式系数用差商表完成
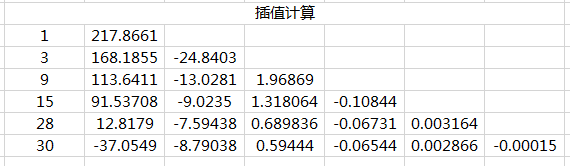
第 1 列是 x,第 2 列是 y。第 3 列计算所有点 (x, y) 与第 1 点 (1, 217.8661) 的斜率,记为 y1。第 4 列计算所有点(x, y1) 与第 1 点 (3, -24.8403) 的斜率,记为 y2。以此类推,更新第 5,6,7 列,直到该列只有一个数
完成差商表后,就得到插值公式了。记阶梯对角上每个数为 A, B, C, D, E, F,第 1 列的每个数为 a, b, c, d, e, f。
结果为:y=A + B*(x-a) + C*(x-a)(x-b) + D*(x-a)(x-b)(x-c) + E*(x-a)(x-b)(x-c)(x-d) + F*(x-a)(x-b)(x-c)(x-d)(x-e)
代码实现:
/*
* @description:插值函数,输入多个数据点,输出对应插值多项式的系数与常数
* @params {Object} points:数据点对象数组 [{x, y}, ...]
* @return {Object}:多项式系数与常数对 [{a, b}, ...]
*/
function interp(points) {
let xRange = points.map(p => p.x)
let yRange = points.map(p => p.y)
let ans = []
ans.push({a: yRange[0], b: 0})
let nextCol = { xRange, yRange }
console.log(nextCol)
while(nextCol.xRange.length >= 2) {
let b = nextCol.xRange[0]
nextCol = diff(nextCol)
console.log(nextCol)
let a = nextCol.yRange[0]
ans.push({ a, b })
}
return ans
}
function diff(col) {
let { xRange, yRange } = col
let nXRange = []
let nYRange = []
for(let i=1; i<xRange.length; i++) {
let newVal = (yRange[i] - yRange[0]) / (xRange[i] - xRange[0])
nXRange.push(xRange[i])
nYRange.push(newVal)
}
return { xRange: nXRange, yRange: nYRange }
}
/*
* 说明:检验插值多项式计算结果
*/
function comInterp(ans, x) {
if(ans.length === 1) return ans[0].a
let result = ans[0].a
let factor = 1
for(let i=1; i<ans.length; i++) {
let {a, b} = ans[i]
factor *= (x - b)
result += a * factor
}
return result
}
自动插值 (autoInterp api)
原理:随机选点,优胜劣汰
/*
* @description:自动插值函数
* @params {Object} oPoints: 数据点对象数组 [{x, y}, ...]
* @params {Number} pCount: 插值数据点数(注:= 多项式次数+1)
* @params {Number} times: 蒙特卡洛试验次数(注:次数越大,精度和时间越高)
* @console :构造数据点,多项式系数&常数,平均误差
*/
function autoInterp(oPoints, pCount=4, times=100000) {
let bestPoints = []
let bestAns = []
let bestE = Infinity
for(let i=0; i<times; i++) {
let points = getRandomPoints(oPoints, pCount)
let ans = interp(points)
let e = checkInterp(ans, oPoints)
if(e < bestE) {
bestPoints = points
bestAns = ans
bestE = e
}
}
console.log(bestPoints)
console.log(bestAns)
console.log(bestE)
}
function comInterp(ans, x) {
if(ans.length === 1) return ans[0].a
let result = ans[0].a
let factor = 1
for(let i=1; i<ans.length; i++) {
let {a, b} = ans[i]
factor *= (x - b)
result += a * factor
}
return result
}
function checkInterp(ans, oPoints) {
return oPoints.reduce((ret, o) =>
ret + Math.abs(o.y - comInterp(ans, o.x)), 0) / oPoints.length
}
function getRandomPoints(oPoints, count) {
oPoints = oPoints.sort((a, b) => .5 - Math.random())
return oPoints.slice(0, count)
}
autoInterp(oPoints, 6, 100000)
暂无评论